Question

A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. (a) if he heads in a direction making an angle ‘$\theta$’ with the flow, find the time he takes to cross the river. (b) Find the shortest possible time to cross the river.

Answer 1

There is a swimmer who wants to cross a river by making an angle ‘$\theta$’ with the flow of the river. We are given the distance and velocity of the river and also the velocity of the swimmer. First we can resolve the components of the velocity of the swimmer and then by using the relation between speed, distance and time we will get the time taken by the swimmer to cross the river.

Formula used: $\text{speed=}\dfrac{\text{distance}}{\text{time}}$

Complete step by step answer:
In the question it is said that a swimmer wishes to swim across a river.
The width and velocity of the river and velocity of the swimmer with respect to water is given to us.
Let ‘d’ be the width of the river, ‘${{v}_{r}}$’ be the velocity of the river and ‘${{v}_{s}}$’ be the velocity of the swimmer. Then we have,
$d=500m$
${{v}_{r}}=5km/h$
$\Rightarrow {{v}_{r}}=5\times \dfrac{5}{18}=\dfrac{25}{18}m/s$
${{v}_{s}}=3km/h$
$\Rightarrow {{v}_{s}}=3\times \dfrac{5}{18}=\dfrac{5}{6}m/s$
In the question it is said that the swimmer heads in a direction making an angle ‘$\theta$’ with the flow of the river.
The figure below represents the given situation.

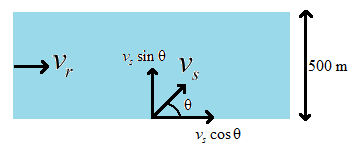
Since the swimmer is swimming with an angle ‘$\theta$’, we resolve the two components of its velocity.
The component of velocity in the x – direction is ${{v}_{s}}\cos \theta$ and the component in the y – direction is ${{v}_{s}}\sin \theta$.
We know that the distance to be covered by the swimmer is in the y – direction. Hence the velocity responsible for the distance covered is ${{v}_{s}}\sin \theta$.
We know that the relation between speed, time and distance is given by the equation,
$\text{speed=}\dfrac{\text{distance}}{\text{time}}$
Therefore we get,
$\Rightarrow {{v}_{s}}\sin \theta =\dfrac{d}{t}$
By substituting the values for ‘${{v}_{s}}$’ and ‘d’ in the equation, we get
$\Rightarrow \dfrac{5}{6}\sin \theta =\dfrac{500}{t}$
Therefore the total time taken to cross the river can be written as,
$\Rightarrow t=\left( \dfrac{500}{\left( \dfrac{5}{6}\sin \theta \right)} \right)$
$\Rightarrow t=\dfrac{500\times 6}{5\sin \theta }$
$\Rightarrow t=\dfrac{600}{\sin \theta }$
Therefore the time taken by the swimmer to cross the river when he swims by making an angle ‘$\theta$’ with the river is $\dfrac{600}{\sin \theta }$ .
We also need to find the shortest possible time to cross the river.
We know that for the shortest time to cross the river, the value of ‘$\theta$’ should be $90{}^\circ$.
Therefore, the shortest time to cross the river will be,
${{t}_{\min }}=\dfrac{600}{\sin 90}$
$\Rightarrow {{t}_{\min }}=\dfrac{600}{1}$
$\Rightarrow {{t}_{\min }}=600\sec$
$\Rightarrow {{t}_{\min }}=\dfrac{600}{60}=10\min$

Thus the minimum time to cross the river is 600 seconds or 10 minutes.

Note: Here we say that for minimum time the angle made by the swimmer with the river is $90{}^\circ$.
For the angle ‘$\theta$’ we have the time as, $t=\dfrac{600}{\sin \theta }$
From this equation we can see that the minimum time will be obtained when the value of $\sin \theta$ is maximum.
We know that the maximum value of $\sin \theta$ is 1 and is obtained when the angle ‘$\theta$’ is $90{}^\circ$.
This is how we take the angle as $90{}^\circ$ for the shortest time to cross the river.