Question

A swimmer S is in the sea at a distance ’d’ km from the closest point A on a straight shore. The house of the swimmer is one the shore at a distance $L{\text{ km}}$ from A. He can swim at a speed of $u{\text{ km/hr}}$ and walk at a speed of $v{\text{ km/hr}}\left( {v > u} \right)$. At which point on the shore should he land so that he reaches his house in the shortest possible time?
A. $\dfrac{{ud}}{{\sqrt {{v^2} - {u^2}} }}$
B. $\dfrac{{vd}}{{\sqrt {{v^2} - {u^2}} }}$
C. $\dfrac{{vd}}{{\sqrt {{v^2} + {u^2}} }}$
D. $\dfrac{{ud}}{{\sqrt {{v^2} + {u^2}} }}$

Answer 1

First of all, draw the figure for this problem with the help of the given data to get a clear idea of what we have to find. Then use the distance-time formula and second derivative test to find the shortest time period. So, use this concept to reach the solution to the given problem.

Complete step-by-step solution:
Given that the swimmer is at a point S which is at a distance ‘d’ km from point A.
Let the house of the swimmer be at point B.
Since the distance between point A and his house i.e., B is $L{\text{ km}}$. So, $AB = L{\text{ km}}$.
Let the swimmer land at point C on the shore and let $AC = x{\text{ km}}$as shown in the below figure:

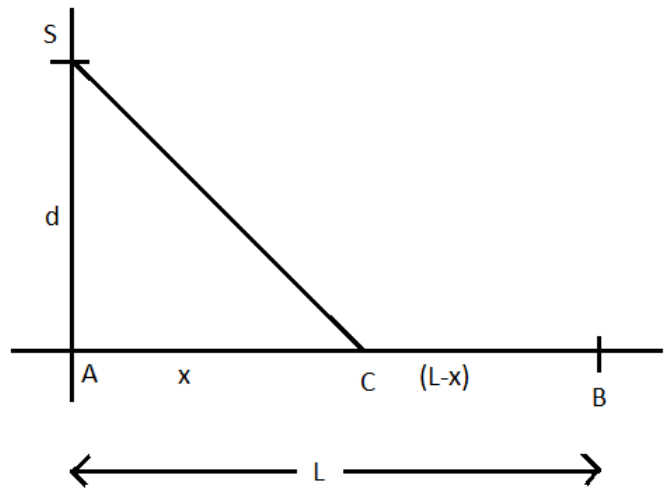
Therefore, from the figure $SC = \sqrt {{x^2} + {d^2}}$ and $CB = \left( {L - x} \right)$
We know that ${\text{time}} = \dfrac{{{\text{distance}}}}{{{\text{speed}}}}$
Given that speed of the swimmer to swim from S to C $= u{\text{ km/hr}}$
So, time taken to travel from S to C $= \dfrac{{\sqrt {{x^2} + {d^2}} }}{u}$
Also given that speed of the swimmer to walk from C to B $= v{\text{ km/hr}}$
So, time taken to travel from S to B $= \dfrac{{L - x}}{v}$
Let $T$ be the time taken to travel from S to B
time taken to travel from S to B = time taken to travel from S to C + time taken to travel from C to B
$\Rightarrow T = \dfrac{{\sqrt {{x^2} + {d^2}} }}{u} + \dfrac{{L - x}}{v}$
Let $f\left( x \right) = T = \dfrac{{\sqrt {{x^2} + {d^2}} }}{u} + \dfrac{L}{v} - \dfrac{x}{v}$
Differentiating $f\left( x \right)$ with respective to $x$, we have

$$\Rightarrow f'\left( x \right) = \dfrac{d}{{dx}}\left( {\dfrac{{\sqrt {{x^2} + {d^2}} }}{u}} \right) + \dfrac{d}{{dx}}\left( {\dfrac{L}{v}} \right) - \dfrac{d}{{dx}}\left( {\dfrac{x}{v}} \right) \\\ \Rightarrow f'\left( x \right) = \dfrac{1}{u}\dfrac{d}{{dx}}\left( {\sqrt {{x^2} + {d^2}} } \right) + \dfrac{d}{{dx}}\left( {\dfrac{L}{v}} \right) - \dfrac{1}{v}\dfrac{d}{{dx}}\left( x \right) \\\ \Rightarrow f'\left( x \right) = \dfrac{1}{u}.\dfrac{{2x}}{{2\sqrt {{x^2} + {d^2}} }} + 0 - \dfrac{1}{v} \\\$$

We know that for the least and greatest value of any function is obtained by equating its first derivate to zero.
For maximum or minimum, put $f'\left( x \right) = 0$

$$\Rightarrow \dfrac{1}{u}.\dfrac{{2x}}{{2\sqrt {{x^2} + {d^2}} }} + 0 - \dfrac{1}{v} = 0 \\\ \Rightarrow \dfrac{x}{{u\sqrt {{x^2} + {d^2}} }} = \dfrac{1}{v} \\\ \Rightarrow \dfrac{{\sqrt {{x^2} + {d^2}} }}{x} = \dfrac{v}{u} \\\$$

Squaring on both sides, we get

$$\Rightarrow \dfrac{{{x^2} + {d^2}}}{{{x^2}}} = \dfrac{{{v^2}}}{{{u^2}}} \\\ \Rightarrow \dfrac{{{x^2}}}{{{x^2}}} + \dfrac{{{d^2}}}{{{x^2}}} = \dfrac{{{v^2}}}{{{u^2}}} \\\ \Rightarrow 1 + \dfrac{{{d^2}}}{{{x^2}}} = \dfrac{{{v^2}}}{{{u^2}}} \\\ \Rightarrow \dfrac{{{d^2}}}{{{x^2}}} = \dfrac{{{v^2}}}{{{u^2}}} - 1 \\\ \Rightarrow \dfrac{{{d^2}}}{{{x^2}}} = \dfrac{{{v^2} - {u^2}}}{{{u^2}}} \\\ \Rightarrow {x^2} = \dfrac{{{u^2}{d^2}}}{{{v^2} - {u^2}}} \\\$$

Rooting on both sides, we have

$$\Rightarrow x = \pm \dfrac{{ud}}{{\sqrt {{v^2} - {u^2}} }} \\\ \therefore x = \dfrac{{ud}}{{\sqrt {{v^2} - {u^2}} }}{\text{ or }}\dfrac{{ - ud}}{{\sqrt {{v^2} - {u^2}} }} \\\$$

We know that, the least value is obtained for the value of $x$ at which $\dfrac{{{d^2}f\left( x \right)}}{{d{x^2}}} > 0$ and the greatest value is obtained for the value of $x$ at which $\dfrac{{{d^2}f\left( x \right)}}{{d{x^2}}} < 0$.
Now, consider the second derivative of $f\left( x \right)$
$\Rightarrow f''\left( x \right) = \dfrac{d}{{dx}}\left( {f'\left( x \right)} \right) = \dfrac{d}{{dx}}\left( {\dfrac{x}{{u\sqrt {{x^2} + {d^2}} }}} \right)$

$$\Rightarrow f''\left( x \right) = \dfrac{d}{{dx}}\left( {f'\left( x \right)} \right) = \dfrac{d}{{dx}}\left( {\dfrac{x}{{u\sqrt {{x^2} + {d^2}} }}} \right) \\\ \therefore f''\left( x \right) = \dfrac{{{d^2}}}{{u\left( {{x^2} + {d^2}} \right)\sqrt {{x^2} + {d^2}} }} \\\$$

For $x = \dfrac{{ud}}{{\sqrt {{v^2} - {u^2}} }}$ we have $f''\left( {\dfrac{{ud}}{{\sqrt {{v^2} - {u^2}} }}} \right) > 0$.
So, the shortest possible time is $\dfrac{{ud}}{{\sqrt {{v^2} - {u^2}} }}$.
Thus, the correct option is A. $\dfrac{{ud}}{{\sqrt {{v^2} - {u^2}} }}$

Note: For the least and greatest value of any function is obtained by equating its first derivate to zero. The least value is obtained for the value of $x$ at which $\dfrac{{{d^2}f\left( x \right)}}{{d{x^2}}} > 0$ and the greatest value is obtained for the value of $x$ at which $\dfrac{{{d^2}f\left( x \right)}}{{d{x^2}}} < 0$.