Question
Question: The shape of any cable is best describe by equation assuming center of a cable is origin, vertical d...
The shape of any cable is best describe by equation assuming center of a cable is origin, vertical direction is taken as positive y-axis and horizontal right taken as positive x-axis?
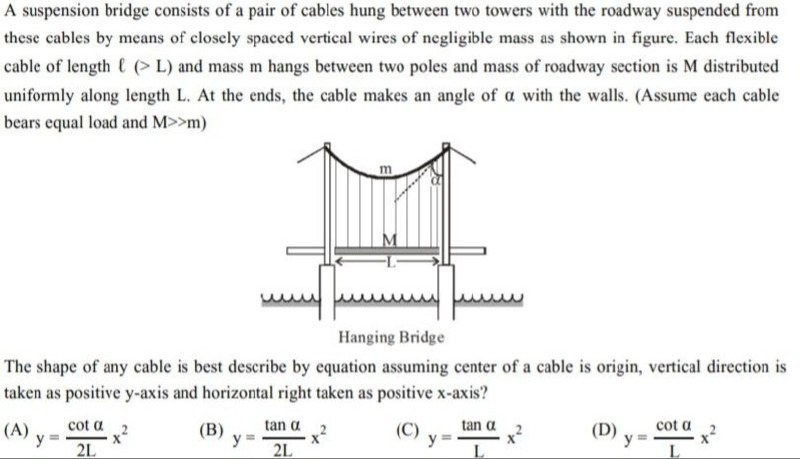
y=2Lcotαx2
y=2Ltanαx2
y=Ltanαx2
y=Lcotαx2
(D) y=Lcotαx2
Solution
To determine the shape of the cable, we analyze the forces acting on a segment of the cable. Given that the mass of the roadway (M) is much greater than the mass of the cable (m), we can neglect the cable's own weight. The load on the cable is primarily due to the roadway, which is distributed uniformly along the horizontal length L.
-
Coordinate System and Load Distribution:
- The origin (0,0) is at the center (lowest point) of the cable.
- The horizontal span of the roadway is L, so the towers are at x=−L/2 and x=L/2.
- There are two cables, and the total roadway mass is M. Each cable bears an equal load, so each cable supports a mass of M/2 over a horizontal length L.
- The linear load density (weight per unit horizontal length) supported by one cable is w=L(M/2)g=2LMg.
-
Equilibrium of a Cable Segment: Consider a segment of the cable from the origin (0,0) to an arbitrary point (x, y).
- Let TH be the horizontal tension in the cable. Since the cable is flexible and the load is purely vertical, the horizontal tension TH is constant throughout the cable.
- The vertical force (weight) supported by the cable segment of horizontal length x is Wx=w⋅x=2LMgx.
- Let θ be the angle the tangent to the cable makes with the horizontal at point (x, y). The slope of the cable at this point is dxdy=tanθ.
For the segment to be in equilibrium, the forces must balance:
- Horizontal forces: The horizontal component of tension at (x,y) must balance TH. So, Tcosθ=TH.
- Vertical forces: The vertical component of tension at (x,y) must balance the weight Wx. So, Tsinθ=Wx.
-
Deriving the Differential Equation: Divide the vertical force equation by the horizontal force equation: TcosθTsinθ=THWx tanθ=THWx Substitute tanθ=dxdy and Wx=2LMgx: dxdy=TH(Mg/2L)x=2LTHMgx
-
Integrating to Find the Cable Shape: Integrate the differential equation with respect to x: y=∫(2LTHMgx)dx y=2LTHMg2x2+C y=4LTHMgx2+C
Since the origin (0,0) is at the lowest point of the cable, when x=0, y=0. 0=4LTHMg(0)2+C⇒C=0. So, the equation of the cable is: y=4LTHMgx2 This equation represents a parabola, which is characteristic of a cable supporting a uniformly distributed horizontal load.
-
Using Boundary Conditions to Find TH: At the ends (towers), the horizontal position is x=L/2. The problem states that the cable makes an angle α with the walls (which are vertical). If the angle with the vertical is α, then the angle with the horizontal, let's call it θend, is 90∘−α. The slope of the cable at the end is dxdyx=L/2. From the differential equation: dxdy=2LTHMgx. At x=L/2: dxdyx=L/2=2LTHMg(2L)=4THMg
We also know that the slope at the end is tanθend=tan(90∘−α)=cotα. Therefore, cotα=4THMg. From this, we can find TH: TH=4cotαMg
-
Final Equation for the Cable Shape: Substitute the expression for TH back into the equation for y: y=4L(4cotαMg)Mgx2 y=4LMgMg4cotαx2 y=Lcotαx2
