Question

A suspended simple pendulum of length $l$ is making an angle $\theta$with the vertical. On releasing, its velocity at the lowest points will be,
$\sqrt {2gl\left( {1 + \cos \theta } \right)}$
$\sqrt {2gl\sin \theta }$
$\sqrt {2gl\left( {1 - \cos \theta } \right)}$
$\sqrt {2gl}$

Answer 1

The mass is attached to an inextensible string and suspended from the fixed support. It is called a simple pendulum. To solve the given problem, consider the positions of the pendulum that is held.
Formula used:
$\Rightarrow \dfrac{1}{2}m{v^2} = mgh$
Where,
$m$is the mass,$v$ is the velocity, $g$ is the acceleration, and $h$ is the height

Complete step by step answer:

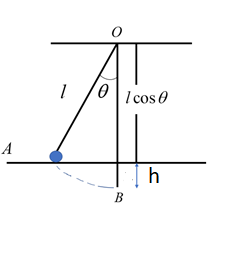
$OA$is given as $l$. Where $l$is the length of the pendulum. $OB$ is given as $l\cos \theta$. In the given diagram the length $l$is making an angle $\theta$ with the vertical.
Calculate the height of the pendulum. We can consider $OA$ and $OB$
$\Rightarrow OB = OA\cos \theta$
$OA$is given as $l$. Substitute the $OA$value in the equation.
$\Rightarrow OB = l\cos \theta$
The height of the pendulum can be calculated as,
$\Rightarrow h = OA - OB$
Substituting the values of the $OA$ and $OB$we get,
$\Rightarrow h = l - l\cos \theta$
Take out $l$ as the common.
$\Rightarrow h = l\left( {1 - \cos \theta } \right)$
Therefore the height of the pendulum is $l\left( {1 - \cos \theta } \right)$.
The velocity of the pendulum released at the lowest point means the velocity of the pendulum when released from $OA$ to $OB$. To calculate the velocity consider the energies at the $A$and $B$.
Consider kinetic energy at $A$and the potential energy at $B$.
Kinetic energy at $A$is equal to the potential energy at $B$
$\Rightarrow \dfrac{1}{2}m{v^2} = mgh$
Where,
$m$is the mass, $v$ is the velocity, $g$ is the acceleration, and $h$ is the height
Cancel out the common terms in the equation.
$\Rightarrow \dfrac{1}{2}{v^2} = gh$
Taking the left-hand side $2$ from the denominator to the right-hand side numerator,
$\Rightarrow {v^2} = 2gh$
Substitute the value of the height in the equation.
$\Rightarrow {v^2} = 2gl\left( {1 - \cos \theta } \right)$
To remove the square on the left-hand side, take the square root on the right-hand side. We get,
$\Rightarrow v = \sqrt {2gl\left( {1 - \cos \theta } \right)}$
Therefore, the value of the simple pendulum on releasing, its velocity at the lowest points will be,
$\Rightarrow v = \sqrt {2gl\left( {1 - \cos \theta } \right)}$

So, the correct answer is “Option C”.

Note:
The pendulum will have one mean position and two extreme positions. At the mean position, the energy of the pendulum is kinetic. At the two extreme positions, the energy of the pendulum is potential. And in between the extreme and mean position the energy is potential plus kinetic.