Question
Question: A surface of the hill is nearly plane with \({30^ \circ }\) slope as shown in figure. From a point \...
A surface of the hill is nearly plane with 30∘ slope as shown in figure. From a point A at a base, a shell is fired using a gun with an initial velocity 30m/s . In the direction making the 60∘angle with the horizontal, the distance AB at which the shell strikes the hill is K×10m . Then find the value of K .
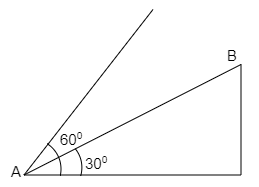
Solution
From the given diagram and the formula, first calculate the angle of the shell with the surface of the hill. Substitute this in the maximum range of the firing formula and the simplification of this provides the value of the distance between the points.
Useful formula:
(1) The angle between the line of bullet and the surface of hill is given by
θ=β−α
Where θ is the angle in which the bullet motion makes with the surface of the hill, β is the angle in which the motion of the bullet makes with the horizontal and α is the slope of the hill.
(2) The distance between two points is given by
d=gcos2α2u2sinθcos(θ+α)
Where d is the distance between two points, u is the initial velocity of the bullet and g is the acceleration due to gravity.
Complete Step by Step Solution:
It is given that the
Slope of the hill, α=30∘
The initial velocity of the bullet, u=30ms−1
The angle in which the motion of the bullet makes with the horizontal, β=600
Using the formula (1),
θ=β−α
θ=60∘−30∘=30∘
Using the formula (2),
d=gcos2α2u2sinθcos(θ+α)
Substituting the known values,
d=9.8×cos230∘2×302×sin30∘cos(30∘+30∘)
K×10=4×9.8×31800×4
By performing the basic arithmetic operation, we get
K=6.12m
Hence the value of K is 6.12m .
Note: Usually the firing the shell is done for the purpose of destroying the huge mass of lands, or killing the enemy in the war. It is also the kind of example of the projectile which follows the curved parabolic path. It is fired by the gun and it moves at some angles with horizontal, when the force gets over it falls on a place.
