Question

A student writes down four conclusions that he observes while performing a polarization experiment with 3 polarisers as shown in the figure. The leftmost and the rightmost polariser are fixed and crossed and the middle one can be rotated. The intensity of the unpolarised light is $I_0$. Identify the incorrect conclusion noted by him.

Answer 1

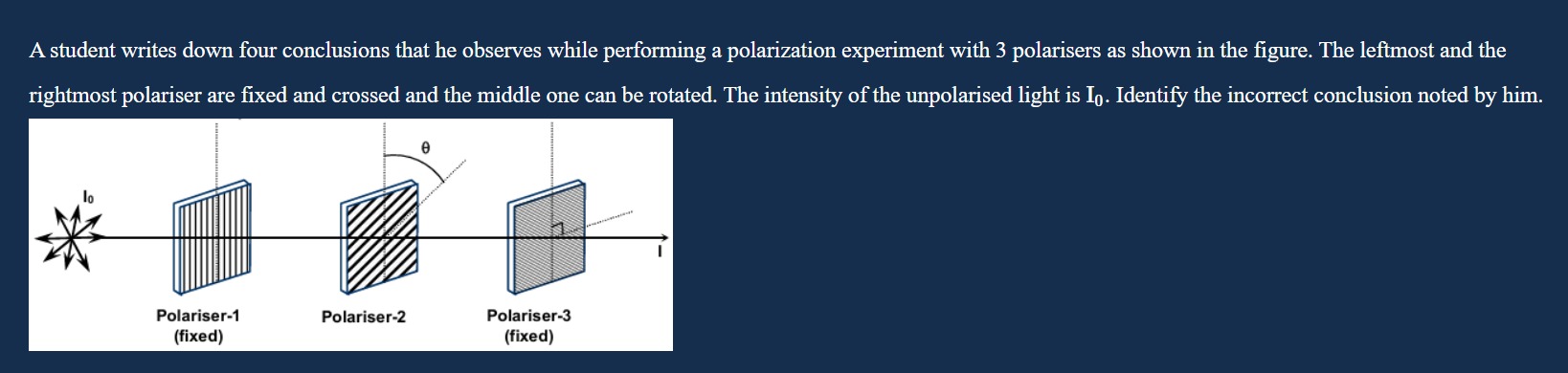
The incorrect conclusion is the one that states that inserting the intermediate polarizer still results in no transmitted light.

Answer 2

Solution:

1. Step 1: When unpolarized light of intensity $I_0$ passes through the first polarizer, it becomes plane polarized with intensity

   $$I_1 = \frac{I_0}{2}.$$

2. Step 2: Let the middle polarizer be at an angle $\theta$ with respect to the first. The transmitted intensity becomes

   $$I_2 = I_1 \cos^2\theta = \frac{I_0}{2}\cos^2\theta.$$

3. Step 3: The third polarizer is fixed perpendicular to the first (i.e. at $90^\circ$), so the angle between the second and third polarizer is $(90^\circ - \theta)$. The final transmitted intensity is

   $$I = I_2 \cos^2(90^\circ - \theta) = \frac{I_0}{2}\cos^2\theta \sin^2\theta.$$

   This can be written as

   $$I = \frac{I_0}{8}\sin^2(2\theta).$$

   Notice that for a proper intermediate angle (say $\theta=45^\circ$) the transmitted intensity is nonzero.

4. Incorrect Conclusion: One common mistaken conclusion is to state that with three polarizers (even if the middle one is rotated) the light would still be completely blocked. In other words, saying “inserting the intermediate polarizer between two crossed polarizers still results in zero transmitted light” is incorrect because the intermediate polarizer actually rotates the polarization direction, permitting a nonzero transmission according to the formula above.

Summary:

• Unpolarized light becomes polarized with $I_1=\frac{I_0}{2}$.
• With the second polarizer at $\theta$: $I_2=\frac{I_0}{2}\cos^2\theta$.
• Third polarizer (at $90^\circ$) yields $I=\frac{I_0}{2}\cos^2\theta\sin^2\theta=\frac{I_0}{8}\sin^2(2\theta)$.
• Therefore, stating that the transmitted light is zero is incorrect.