Question

A student was given the experiment to measure the emf of an unknown cell using a potentiometer. He cheated the result and wrote the observation arbitrarily and was caught. Which reading helped the teacher to arrive at the conclusion that he cheated $?$

S. No.	Value of rheostat	Null point
$1.$	${R_1}$	$50\,cm$
$2.$	${R_2}$	$60\,cm$
$3.$	${R_3}$	$70\,cm$ $$
$4.$	${R_4}$	$80\,cm$

$\left( A \right)\,\,1 \\\ \left( B \right)\,\,2 \\\ \left( C \right)\,\,3 \\\ \left( D \right)\,\,4 \\\$

Answer 1

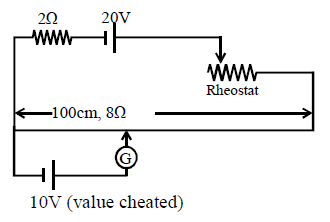
In the given diagram, actual value of the voltage and resistance are given. By using the equation of ohm’s law we calculate all the actual values of the resistance and also we find the cheated values in the above table.

Formulae Used:
The expression for finding the current is
$I\, = \,\dfrac{V}{\operatorname{R} }$
Where
$I$ be the current of the cell, $V$ be the voltage of the cell and $R$ be the Resistance of the cell.

Complete step-by-step solution :
We know that actual voltage $v\, = 20\,volts$
Cheated voltage $v\, = \,10\,volts$
Resistance of the cells are $2\,\Omega \,$and $8\,\Omega$ (Resistance is measured in ohms $\left( \Omega \right)$)
$I\, = \,\dfrac{V}{R}.........\left( 1 \right)$
Substitute the known values in the equation $\left( 1 \right)$
$I\, = \,\dfrac{{20\,V}}{{8 + 2 + R}}$
Perform the arithmetic operations in the above equation we get,
$I\, = \,\dfrac{{20}}{{10 + R}}$
In the figure, we know that null point is at $8\,\Omega$
Distance $d$ is $100\,cm$ and length $l\,is\,l\,cm$.
So, $\dfrac{{8 \times l}}{{100}}\,i\, = \,10$
Simplify the above equation we get,
$li\, = \,125$
From above equations,
$\dfrac{1}{{10 + R}}\, = \,6.25$
Simplify the equation we get,
$R\, = \,\dfrac{1}{{6.25}} - 10$ $> \,0$
Hence, $I\,is\,\,62.5\, > 0$
So from the above option, the option $\left( C \right)$ is correct.
Therefore, the value of ${R_1}$ and ${R_2}$ violate the conditions.

Note:- In the question, the value of voltage is high. So we get the value of rheostat is high. But, the cheated value is half of the given value. So there must be a difference in the value of rheostat. From the table the value of rheostat is high. So, thus the value of the rheostat must be low if the voltage is low.