Question
Question: A student traces the path of a ray of light through a rectangular glass slab for the different value...
A student traces the path of a ray of light through a rectangular glass slab for the different values of angle of incidence. He observes all possible precautions at each step of the experiment. At the end of the experiment, on analyzing the measurements, which of the following is he likely to draw?
A. ∠i=∠e<∠r
B. ∠i<∠e<∠r
C. ∠i>∠e>∠r
D. ∠i=∠e>∠r
Solution
Hint: Use Snell’s law i.e. μ1sini=μ2sinr , where i is the angle of incidence and r is the angle of refraction at the interface of the two mediums. μ1 is the refractive index of the medium where the light is incident and μ2 is the refractive index of the medium where the light gets refracted. Use this formula at both the parallel surfaces of the glass.
Formula used:
μ1sini=μ2sinr
Complete step-by-step answer:
A glass slab is in cuboidal shape (opposite surfaces parallel to each other). Let us understand what happens when a light ray enters a glass slab. When a light ray passes through a glass slab it is refracted twice at the two parallel faces and finally emerges parallel to its incident direction.
Suppose a light ray enters the glass slab from air. It will first be refracted at this surface.
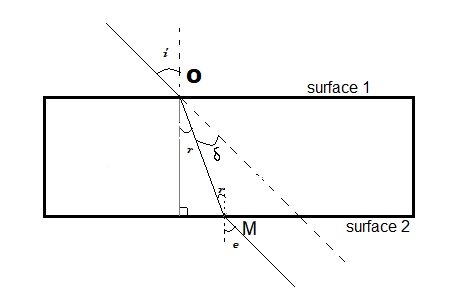
Use Snell’s law i.e. μ1sini=μ2sinr.
⇒1.sini=(1.5).sinr …….(1) (Refractive indices of air and glass are 1 and 1.5 respectively)
Since the light is entering a denser medium, it will bend towards the normal at the interface of air and the glass slab (surface 1).
This implies that the angle of incidence is greater than the angle of refraction i.e. i > r.
Afterwards, the refracted ray will travel through the glass and will be incident on the opposite surface.
Here, as you can see in the given figure, the angle of incident at surface 2 will be equal to the angle of refraction at surface 1 (since the normals at points O and M at the two surfaces are parallel).
Let the angle of refraction at surface two be ‘e’. Now, use Snell’s law.
⇒1.sine=(1.5)sinr …….(2)
Compare equations (1) and (2). We get, i=e.
Hence, the emergent ray is parallel to the incident ray.
Hence, we conclude that i = e > r.
Therefore, the correct option is D.
Note: The relation between i, e and r (i.e. i = e > r) that we found is not always true. When the light exits the glass medium at surface 2, if angle of refraction is more than the critical angle then the light, the refraction is so much that the light is internally reflected back into the glass medium. And e=0.
