Question

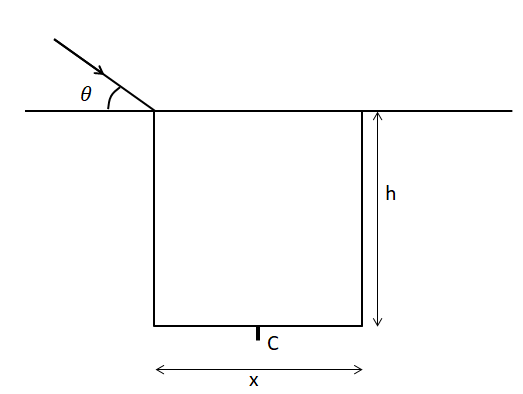
A student sees the top edge and the bottom center C of a pool simultaneously from an angle $\theta$ above the horizontal as shown in the figure. The refractive index of water which fills up to the top edge of the pool is 4/3. If h/x = 7/4 then $\cos \theta$ is

$A.\quad \dfrac{2}{7}$
$B.\quad \dfrac{8}{3\sqrt{45}}$
$C.\quad \dfrac{8}{3\sqrt{53}}$
$D.\quad \dfrac{8}{21}$

Answer 1

Hint: This problem needs concepts refraction and trigonometric identities to solve this problem. Snell's law,${{n}_{1}}\sin i={{n}_{2}}\sin r$ is required in solving this problem. The basic trigonometry and Pythagoras theorem is essential too.

Step by step solution:
Let’s make a detailed diagram from the image given to better understand the problem.

We know that when a ray passes from a rarer medium to the denser medium, the ray bends towards the normal. Here the student is watching from top. Hence, the upper medium from where the ray is incident, or from where the student watches the pool is in air having the refractive index 1. That is, ${{n}_{1}}=1$. The ray upon entering the pool bends towards the normal, having a refractive index is, ${{n}_{2}}=\dfrac{4}{3}$. The ray is incident with an angle (i) with respect to the normal and the angle (r) is the angle of refraction with respect to the normal.

Now, we will use Snell's law, which is given by, ${{n}_{1}}\sin i={{n}_{2}}\sin r$.
Putting in the value of ${{n}_{1}}=1$and ${{n}_{2}}=\dfrac{4}{3}$into the Snell’s law, we get, $1\times \sin i=\dfrac{4}{3}\times \sin r\Rightarrow \sin i=\dfrac{4}{3}\sin r\to (1)$
Now, let’s consider the right angled triangle created at the bottom of the pool by the refracted ray, the side of the rectangular pool and the bottom of the rectangular pool.
Using the Pythagoras theorem, $side{{(1)}^{2}}+side{{(2)}^{2}}=hypotenuse{{e}^{2}}$. Side(1) is the pool’s height (h) and side(2) is the distance of the bottom of the pool from the point C.
Hence, ${{h}^{2}}+{{(\dfrac{x}{2})}^{2}}=hypotenuse{{e}^{2}}\Rightarrow hypotenuse=\sqrt{{{h}^{2}}+{{\dfrac{x}{4}}^{2}}}$.

For this triangle, we get $\sin r=\dfrac{\dfrac{x}{2}}{hypotenuse}\Rightarrow \sin r=\dfrac{\dfrac{x}{2}}{\sqrt{{{h}^{2}}+{{\dfrac{x}{4}}^{2}}}}\Rightarrow \sin r=\dfrac{\dfrac{x}{2}}{x\sqrt{{{(\dfrac{h}{x})}^{2}}+\dfrac{1}{4}}}\Rightarrow \sin r=\dfrac{1}{2\sqrt{{{(\dfrac{h}{x})}^{2}}+\dfrac{1}{4}}}$.

We are given the ratio h/x to be equal to 7/4. Substituting in this value in the above equation we get,
$\sin r=\dfrac{1}{2\sqrt{{{(\dfrac{7}{4})}^{2}}+\dfrac{1}{4}}}\Rightarrow \sin r=\dfrac{1}{2\sqrt{\dfrac{49}{16}+\dfrac{1}{4}}}\Rightarrow \sin r=\dfrac{1}{2\sqrt{\dfrac{53}{16}}}\Rightarrow \sin r=\dfrac{1}{\dfrac{2}{4}\sqrt{53}}\Rightarrow \sin r=\dfrac{2}{\sqrt{53}}$.
Hence, we get the value of sin(r). Now let’s consider the angles on the top, $i+\theta =\dfrac{\pi }{2}\Rightarrow i=\dfrac{\pi }{2}-\theta$. Therefore, sin(i) becomes, $\sin i=\sin (\dfrac{\pi }{2}-\theta )=\cos \theta$.

Putting these values of sin(i) and sin(r) into eqn(1) we get, $\cos \theta =\dfrac{4}{3}\times \dfrac{2}{\sqrt{53}}\Rightarrow \cos \theta =\dfrac{8}{3\sqrt{53}}$.

Hence, the value $\cos \theta =\dfrac{8}{3\sqrt{53}}$

Note: Making a proper ray diagram of the question is also necessary to help us in finding out $\cos \theta$.
Further, we must also remember how the light ray bends when it moves from one medium to another. When, the light moves from a rarer medium to a denser medium. The light ray bends towards the normal and when the light ray mover from denser medium to a rarer medium, the light ray moves away from the normal.