Question
Question: A student is experimenting with a resonance tube apparatus in a Physics lab to find the speed of sou...
A student is experimenting with a resonance tube apparatus in a Physics lab to find the speed of sound at room temperature. He got resonating lengths of air columns as 17cm and 51cm, using tuning forks of frequency 512Hz. Find speed of sound at the room temperature and specify, whether the side water reservoir was moved upward or downward to obtain the second resonance (51cm)?
A. 348 m/s, downwards
B. 348 m/s, upwards
C. 332 m/s, downwards
D. 332 m/s, upwards
Solution
The resonance tube is considered to be an open organ pipe. So, for first resonance, there is one node and one antinode, whose length is a quarter of the wavelength of the sound wave. The water inside the reservoir will move upward, as the resonances increase, successively.
Formula used:
f1=4L1vs
Complete answer:
First let us draw a rough diagram of resonance tube apparatus. It is mentioned in the problem that the student got resonating columns at 17cm and 51cm. This indicates that at 17cm the first resonance occurs and at 51cm the second resonance occurs.
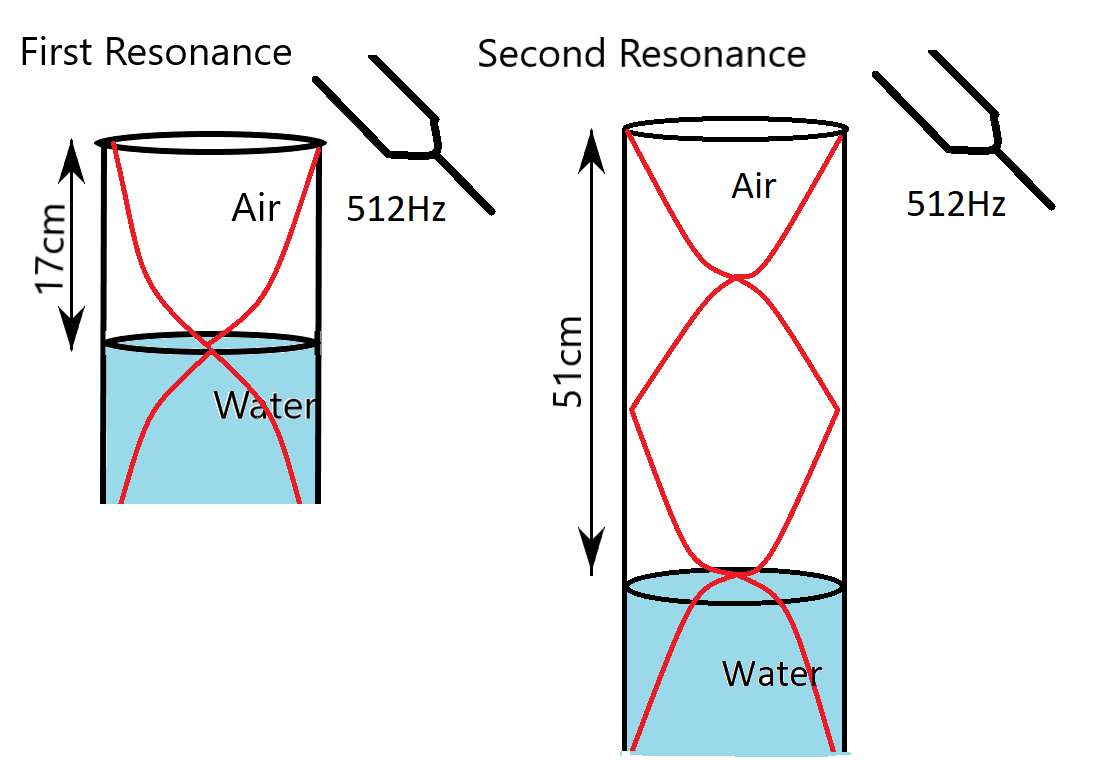
The condition for first resonance is
f1=4L1vs
Where
f1 is the first resonance frequency
vs is the velocity of the sound
L1 is the length at which first resonance occurs
We have f1= 512Hz and L1= 17cm. Substituting this in the first resonance condition
\eqalign{
& {f_1} = \dfrac{{{v_s}}}{{4{L_1}}} \Rightarrow {v_s} = {f_1} \times 4{L_1} \cr
& \Rightarrow {v_s} = 512 \times 4\left( {17 \times 1{0^{ - 2}}} \right) = 348.16m{s^{ - 1}} \cr
& \therefore {v_s} = 348.16m{s^{ - 1}} \sim 348m{s^{ - 1}} \cr}
Now, for the second part of the answer, we have actually increased the air column compared to the first resonance. So, the water level would have reduced, in the resonance tube. This will compensate as an increase of water level in the side water reservoir. This shows as an upward movement of water in the side water reservoir.
So, the correct answer is “Option B”.
Note:
The above problem can also be solved using the condition for second resonance i.e.,
f2=4L23vs
Where
f2 is the second resonance frequency
vs is the velocity of the sound
L2 is the length at which second resonance occurs.
Substituting the values given, we have
\eqalign{
& {f_2} = \dfrac{{3{v_s}}}{{4{L_2}}} \cr
& \Rightarrow {v_s} = {f_2} \times \dfrac{{4{L_2}}}{3} \cr
& \Rightarrow {v_s} = 512Hz \times \dfrac{{4 \times \left( {51 \times {{10}^{ - 2}}} \right)}}{3} =348.16m{s^{ - 1}} \cr
& \therefore {v_s} = 348.16m{s^{ - 1}} \sim 348m{s^{ - 1}} \cr}
