Question

A student has a freedom to study any subject of his choice. In a group of students with number 1 to 300, the students whose number is divisible by 3 select arts faculty. The students whose number is divisible by 5 select commerce faculty and the students whose number is divisible by 10 select science faculty. Find the number of students who select only one faculty.

Answer 1

Calculate the number of students who selected arts faculty, commerce, faculty, then find the students who are in the intersection of two sets and then the intersection of three sets. Draw the corresponding Venn-diagram and find the number of students who selected only one faculty.

Complete step-by-step answer:
We are given that students have numbers from 1 to 300.
Let $n\left( A \right)$ be the number of students who select arts faculty, $n\left( B \right)$ be the number of students who select commerce faculty, and $n\left( C \right)$ be the number of students who select science faculty.
That is for $n\left( A \right)$, we have to find the numbers from 1 to 300 that are divisible by 3
Hence, there are $\dfrac{{300}}{3} = 100$ such numbers.
Similarly, $n\left( B \right) = \dfrac{{300}}{5} = 60$ numbers divisible by 5.
And $n\left( C \right) = \dfrac{{300}}{{10}} = 30$ numbers divisible by 10.
The numbers which are divisible by 3 and 5 will be the numbers that are divisible by 15.
$n\left( {A \cap B} \right) = \dfrac{{300}}{{15}} = 20$ students.
The numbers which are divisible by 3 and 10 are the numbers which are divisible by 30
$n\left( {A \cap C} \right) = \dfrac{{300}}{{30}} = 10$ students.
Also, the numbers which are divisible by 5 and 10 are the numbers which are divisible by 10
$n\left( {B \cap C} \right) = \dfrac{{300}}{{10}} = 30$ students.
And, now find the numbers that are divisible by all three numbers, that is numbers will be divisible by 30
$n\left( {A \cap B \cap C} \right) = \dfrac{{300}}{{30}} = 10$ students.
Now, draw the Venn diagram of the information.

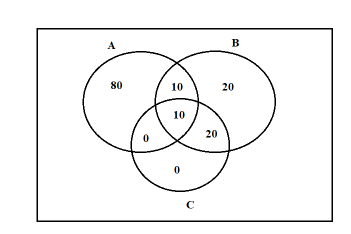
Now, we want to find the number of students that have only one faculty.
$80 + 20 + 0 = 100$
There are 100 students who selected only one faculty.

Note: Many students make mistakes in drawing the corresponding Venn-diagram. While drawing the Venn- diagram, be sure that all that the whole set $A$ includes only $A$, $A \cap B$, $A \cap C$ and $A \cap B \cap C$. Always start writing elements from the intersection of all three sets, then the intersection of two sets and so on.