Question

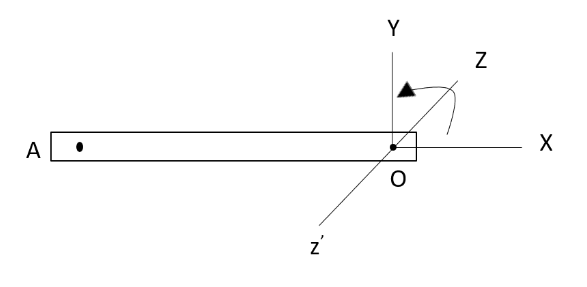
A strip length $1m$ rotates about the Z-axis passing through the point O in the X-Y plane with an angular velocity of $10{\text{ }}rad/s$ in the counterclockwise direction, and O is at rest. The velocity of point A is:

A. $10km/s$
B. $- 10\widehat Jm/s$
C. $+ 10\widehat Jm/s$
D. $100\widehat Km/s$

Answer 1

Angular velocity is the rate of change of the angular position of a rotating body, the angle is changed over time. The unit of angular velocity is $rad/s,$ while linear velocity is speed in a straight line, its units are $m/s$. So, here to solve the question we have taken the formula of relation between linear velocity and angular velocity, and by putting the value in the formula, we will get our required answer.

Complete step by step answer:
We have been given that a strip AO of length $1m$ that rotates about the Z-axis passing through the point O in the X-Y plane with an angular velocity of $10{\text{ }}rad/s$ in the counterclockwise direction, and O is at rest, while A is moving. We need to find the velocity of point A with which it is moving.
We know that, the relation between linear velocity and angular velocity is, $V = \omega \times l$
where, V $=$ linear velocity
$\omega {\text{ }} =$ angular velocity
l $=$ length of strip
We have been given angular velocity, $\omega = - 10\widehat J/s$ and length of strip, $l{\text{ }} = {\text{ }}1m.$
So, on putting the given values in the above formula, we get

$${\overrightarrow {{V_A}} {\text{ }} = {\text{ }} - 10\widehat J/s \times 1m} \\\ { = {\text{ }} - 10\widehat Jm/s}$$

Thus, option (B) is correct.

Note: Students should note that in the solutions above we have taken angular velocity, $\omega = - 10\widehat J/s$, the value is negative because the strip is rotating counterclockwise direction, and in that we consider the negative values.