Question

A string passing over a smooth light pulley connects two blocks of masses ${{\text{m}}_{\text{1}}}\text{ and }{{\text{m}}_{\text{2}}}$ where (${{\text{m}}_{\text{1}}}\text{}{{\text{m}}_{\text{2}}}$ ). The masses are moving vertically. If the acceleration of the system is g/8 then:
This question has multiple correct options
$\begin{aligned} & a)\dfrac{{{m}_{1}}}{{{m}_{2}}}=\dfrac{9}{7} \\\ & b)\dfrac{{{m}_{1}}}{{{m}_{2}}}=\dfrac{4}{3} \\\ & c)\text{tension in the string=}\dfrac{3}{4}{{m}_{1}}g \\\ & d)\text{tension in the string=}\dfrac{9}{8}{{m}_{2}}g \\\ \end{aligned}$

Answer 1

It is given in the question that ${{\text{m}}_{\text{1}}}\text{}{{\text{m}}_{\text{2}}}$ hence ${{\text{m}}_{\text{1}}}$ will move vertically downwards and ${{\text{m}}_{\text{2}}}$ will move vertically upwards. Both the masses are connected to a common string and hence both of them will move with a common acceleration. Hence will draw the free body diagram of the above system and find the ratio of the masses and the tension in the string to verify with the given options.

Complete answer:
To begin with let us first draw the free body diagram and obtain the net force on each of the masses.

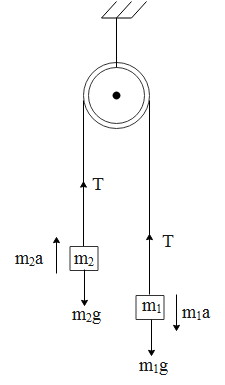
If we see the above free body diagram the mass ${{m}_{1}}$ moves downwards, while the mass ${{m}_{2}}$ moves upwards. Both of the masses move with common acceleration i.e. a. The net force on mass ${{m}_{1}}$ is,
${{m}_{1}}a={{m}_{1}}g-T...(1)$ where g is the acceleration due to gravity and T is the tension in the rope. Similarly, the net force on ${{m}_{2}}$ is given by, ${{m}_{2}}a=T-{{m}_{2}}g...(2)$ where g is the acceleration due to gravity and T is the tension in the rope.

Adding both the equations 1 and 2 we get,
$\begin{aligned} & \Rightarrow {{m}_{1}}a+{{m}_{2}}a={{m}_{1}}g-T+T-{{m}_{2}}g \\\ & \Rightarrow a({{m}_{1}}+{{m}_{2}})=({{m}_{1}}-{{m}_{2}})g,\text{since a=g/8} \\\ & \Rightarrow \dfrac{g}{8}({{m}_{1}}+{{m}_{2}})=({{m}_{1}}-{{m}_{2}})g \\\ & \Rightarrow \dfrac{{{m}_{1}}}{8}+\dfrac{{{m}_{2}}}{8}={{m}_{1}}-{{m}_{2}} \\\ & \Rightarrow {{m}_{1}}\left( \dfrac{1}{8}-1 \right)=-{{m}_{2}}\left( 1+\dfrac{1}{8} \right) \\\ & \Rightarrow {{m}_{1}}\left( -\dfrac{7}{8} \right)=-{{m}_{2}}\left( \dfrac{9}{8} \right) \\\ & \implies \dfrac{{{m}_{1}}}{{{m}_{2}}}=\dfrac{9}{7} \\\ \end{aligned}$

Dividing equation 1 by 2 we get,
$\begin{aligned} & \Rightarrow \dfrac{{{m}_{1}}a}{{{m}_{2}}a}=\dfrac{{{m}_{1}}g-T}{T-{{m}_{2}}g} \\\ & \Rightarrow \dfrac{{{m}_{1}}}{{{m}_{2}}}=\dfrac{{{m}_{1}}g-T}{T-{{m}_{2}}g} \\\ & \Rightarrow {{m}_{1}}T-{{m}_{1}}{{m}_{2}}g={{m}_{2}}Mg-T{{m}_{2}} \\\ & \Rightarrow {{m}_{1}}T+T{{m}_{2}}={{m}_{2}}{{m}_{1}}g+{{m}_{1}}{{m}_{2}}g \\\ & \Rightarrow T({{m}_{1}}+{{m}_{2}})=2{{m}_{2}}{{m}_{1}}g \\\ & \Rightarrow T=\dfrac{2{{m}_{2}}{{m}_{1}}g}{{{m}_{1}}+{{m}_{2}}}\text{N dividing the equation by }{{m}_{1}}\text{we get,} \\\ & \Rightarrow T=\dfrac{\dfrac{2{{m}_{2}}{{m}_{1}}g}{{{m}_{1}}}}{\dfrac{{{m}_{1}}+{{m}_{2}}}{{{m}_{1}}}}\text{ } \\\ & \implies T=\dfrac{2{{m}_{2}}g}{1+\dfrac{{{m}_{2}}}{{{m}_{1}}}}\text{ since}\dfrac{{{m}_{1}}}{{{m}_{2}}}=\dfrac{9}{7}, \\\ & \implies T=\dfrac{2{{m}_{2}}g}{1+\dfrac{7}{9}}=\dfrac{2{{m}_{2}}g}{\dfrac{16}{9}}=\dfrac{9}{8}{{m}_{2}}g \\\ \end{aligned}$

So, the correct answer is “Option A and D”.

Note:
It is to be noted that the above thread is assumed to be mass less. Hence we can conclude that the tension at every point on the thread is constant. But in reality the thread also has mass, as a result the tension along the thread will be more at higher points from the point where the mass is attached to the thread.