Question
Question: A string of negligible mass over a clamped pulley of mass \(m\) supports a block of mass \(M\) as sh...
A string of negligible mass over a clamped pulley of mass m supports a block of mass M as shown in the figure. The force on the pulley by the clamp is given as:
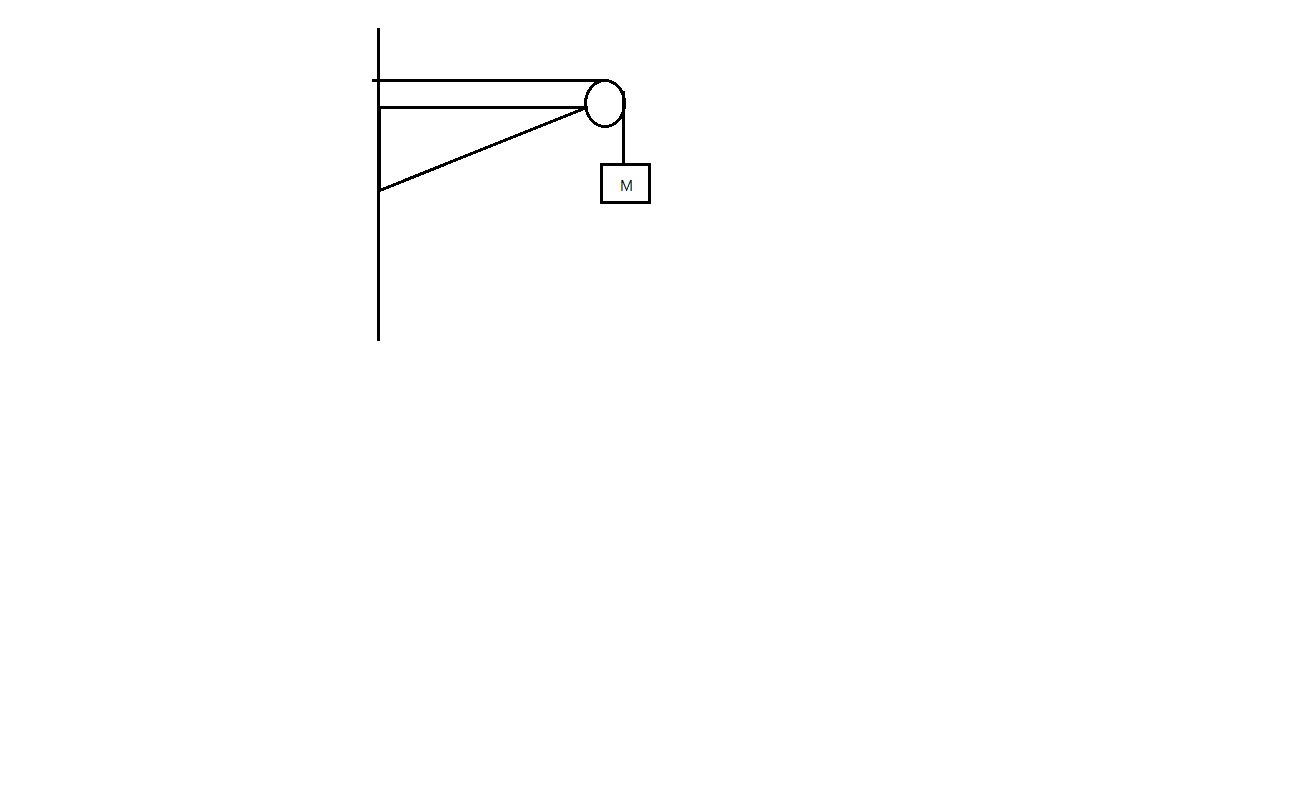
Solution
We can assume the pulley-mass to be a system. There are two forces which act on the system. One is the tension on the string, and the other is the force due to gravitation. Then the resultant vector is the force acting on the whole system.
Formula used:
F=(m+M)g and T=mg
Complete step-by-step answer:
We know that a pulley is a simple device that can lift heavy objects with minimum energy. Here a block of some mass is attached to the pulley. A pulley consists of a tensile string or rope, which is used to tie and lift the heavy body and a shaft above which the string is kept. The shaft is circular generally and allows the easy movement of the string.
The force needed to lift the massive body is greater than the force needed to pull it using a pulley.Hence pulleys are used to lift heavy objects
Consider the pulley-mass system as shown in the figure. Where M is the mass of the block and m is mass of the pulley. Let T be the tension on the string and F be the force due to gravitation.
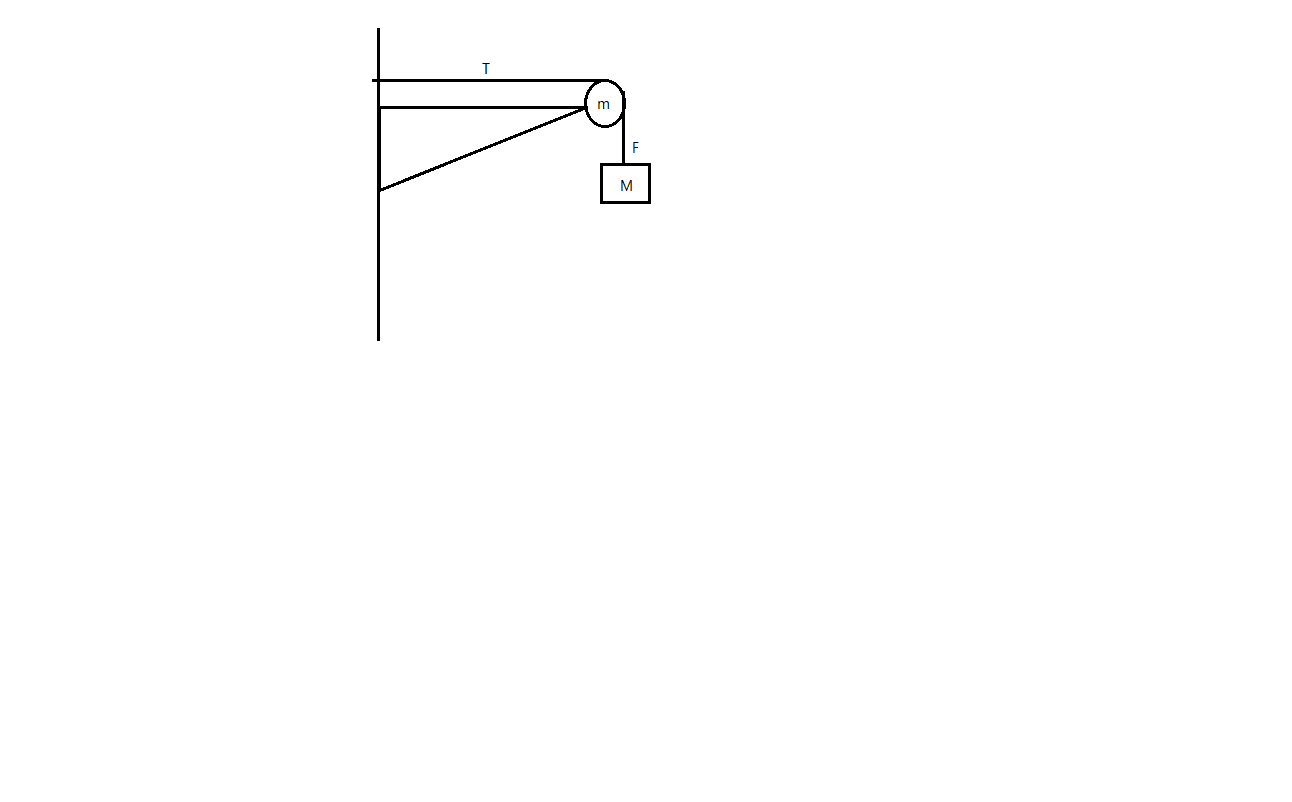
Then clearly T=mg and F=(m+M)g, and both are vectors. Then by vector addition we can say that, the R is the resultant force on the pulley and is given as R=T+F
Then the magnitude of the resultant force is given as ∣R∣=((M+m)g)2+(Mg)2=g(M+m)2+M2
Thus the requires answer is ∣R∣=((M+m)g)2+(Mg)2=g(M+m)2+M2
So, the correct answer is “Option A”.
Note: The direction of T and F are x^ and −y^ respectively. Hence the direction of the resultant force, will be the addition of the two vectors using the parallelogram law of addition. Here only the force on the pulley is asked, hence the magnitude is sufficient.
