Question
Question: A string of negligible mass going over a clamped pulley of mass m, supports a block of mass M as sho...
A string of negligible mass going over a clamped pulley of mass m, supports a block of mass M as shown in the figure. The force on the pulley by the clamp is given by :
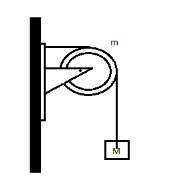
A. 2Mg
B. 2mg
C. (M+m)2+m2g
D. ((M+m)2+m2)g
Solution
In this problem you need to draw the free body diagram denoting all the forces and we know that the forces are in equilibrium that is why the system is not moving so we will make the equation equating the forces in equilibrium with equal and opposite forces then we will get force on the pulley. Doing this will give us the right answer.
Complete answer:
The figure with all the forces is:
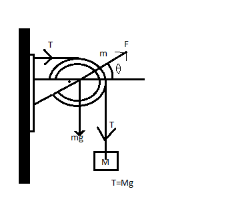
We can clearly see from the figure above that the system is in equilibrium.
It is said that a string of negligible mass going over a clamped pulley of mass m, supports a block of mass M as shown in the figure. We need to find the force on the pulley by the clamp.
So, we will equate the equal and opposite forces.
From the figure we can clearly see that,
⇒Fcosθ=Mg (The horizontal force)………….(1)
⇒Fsinθ=(M+m)g (Vertical forces)……………..(2)
We need to calculate the value of the force F so we will square the equation (1) and the equation (2) and add.
So, we do,
So, we get the value of the force by the clamp as ((M+m)2+m2)g.
So, the correct answer is “Option D”.
Note:
When you get to solve such problems then drawing the diagram with all the forces is a must and we also need to know that if the system is at rest then the forces are in equilibrium and we can find the unknown term with the help of those forces. Doing this will solve your problems and will give you the right answer.
