Question
Question: A string of length \[L\] is fixed at one end and carries a mass, \[M\] at the other end. The string ...
A string of length L is fixed at one end and carries a mass, M at the other end. The string makes 2/π revolutions per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is
A. ML
B. 2ML
C. 4ML
D. 16ML
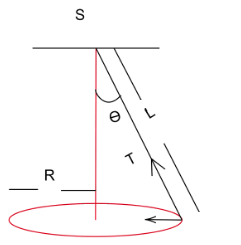
Solution
We are asked to find the tension in the string with respect to the length of the string and the mass carried at the other end. We start by noting down the given data from the question. Then we use the formula of finding the angular frequency and use it to determine the angular frequency from the given value of frequency. After the value of angular frequency is found, we move onto finding the tension of the string with respect to the mass fixed at the other end, the length of the string and the angular frequency. This gives us the right solution to this question.
Formulas used:
The tension of the string is given by the formula, T=MLω2
The angular frequency is given by the formula, ω=2πf
Where, L is the length of the given string, M is the mass attached to the other end of the string and f is the frequency of the motion.
Complete step by step answer:
We start by writing down the given information in the question, L is the length of the given string and M is the mass attached to the other end of the string.
The frequency of the motion is given as,
f=π2rev/s
We are given the frequency of the motion, with this, we find the angular frequency of the motion by using the formula,
ω=2πf
Substituting with the values we get,
\Rightarrow \omega = 2\pi \times \dfrac{2}{\pi } \\\ \Rightarrow \omega = 4$$ Now that we have the value of the angular frequency, we can find the value of tension by substituting in the formula, $$T = ML{\omega ^2}$$ We get $$T = ML{\omega ^2} \\\ \Rightarrow T= ML{4^2} \\\ \therefore T= 16ML$$ **Hence, the right answer is option D.** **Note:** This problem can also be done by taking the tension equivalent to the centripetal force. That is, $$T = \dfrac{{m{v^2}}}{r}$$ We can then find the tangential velocity of the motion by the cross-multiplication method $$1rev \Rightarrow 2\pi L$$ For the given angular frequency, we multiply both the sides with $$\dfrac{2}{\pi }$$ and get the value of tangential velocity as, $$4L$$ Now we substitute the value of tangential velocity in the formula and get, $$T = \dfrac{{M{{\left( {{v_{\tan }}} \right)}^2}}}{L} \\\ \Rightarrow T= \dfrac{{M \times 16{L^2}}}{L} \\\ \therefore T= 16ML$$