Question
Question: A string is wrapped around the rim of a wheel of moment of inertial \[0.20\,{\text{kg}} \cdot {{\tex...
A string is wrapped around the rim of a wheel of moment of inertial 0.20kg⋅m2 and radius 20cm. The wheel is free to rotate about its axis. Initially the wheel is at rest. The string is now pulled by a force of 20N. The angular velocity of the string after 5 seconds will be:
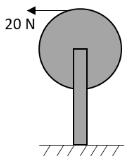
A. 90rad/s
B. 70rad/s
C. 95rad/s
D. 100rad/s
Solution
Use the formula for torque acting on an object due to a force and torque acting on an object in terms of the moment of inertia and angular acceleration of the object. Also use the kinematic equation for the final angular velocity of an object in terms of angular acceleration. First calculate the angular acceleration of the wheel and then angular velocity of the wheel after 5 seconds.
Formulae used:
The torque τ acting on an object due to a force F is
τ=Fr …… (1)
Here, r is the perpendicular distance between the point of action of the force and centre of torque.
The torque τ acting on an object is
τ=Iα …… (2)
Here, I is the moment of inertia of the object and α is angular acceleration of the object.
The kinematic equation for the final angular velocity ω of an object in terms of angular acceleration α is
ω=ω0+αt …… (3)
Here, ω0 is the initial angular velocity of the object and t is time.
Complete step by step answer:
We have given that the moment of inertia of the wheel is 0.20kg⋅m2 and the radius of the wheel is 20cm.
I=0.20kg⋅m2
R=20cm
The string wrapped around the rim of the wheel is pulled by a force 20N.
F=20N
We have asked to calculate the angular velocity of the wheel after 5 seconds.Let us first calculate the angular acceleration of the wheelSubstitute Iα for τ in equation (1).
Iα=FR
⇒α=IFR
Substitute 20N for F, 20cm for R and 0.20kg⋅m2 for I in the above equation.
⇒α=0.20kg⋅m2(20N)(20cm)
⇒α=0.20kg⋅m2(20N)(0.20m)
⇒α=20rad/s2
Hence, the angular acceleration of the wheel is 20rad/s2.
Let us now calculate the velocity of the wheel after 5 seconds.Initially the wheel starts from rest. Hence, the initial angular velocity of the wheel is 0rad/s.
ω0=0rad/s
We can calculate the angular velocity after 5 seconds using equation (3).Substitute 0rad/s for ω0, 20rad/s2 for α and 5s for t in equation (3).
ω=(0rad/s)+(20rad/s2)(5s)
∴ω=100rad/s
Therefore, the angular velocity of the wheel after 5 seconds is 100rad/s.
Hence, the correct option is D.
Note: The students can also calculate the angular velocity of the wheel after 5 seconds by directly using the formula for the angular acceleration in terms of angular velocity and time as the wheel is initially at rest. But the students should keep in mind that we can directly use the formula for angular acceleration only when the initial velocity of the object is zero, otherwise not.
