Question

A string is wound around a hollow cylinder of mass $5kg$ and radius $0.5m$ . If the string is now pulled with a horizontal force of $40N$ and the cylinder is rolling without slipping on a horizontal surface (see figure), then the angular acceleration of the cylinder will be? (Neglect the mass and thickness of the string)

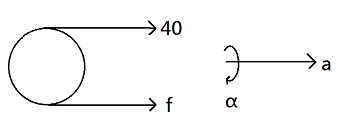
A) $12\,rad\,{s^{ - 2}}$
B) $16\,rad\,{s^{ - 2}}$
C) $10\,rad\,{s^{ - 2}}$
D) $20\,rad\,{s^{ - 2}}$

Answer 1

The forces in horizontal direction are the force of $40N$ and the frictional force. Apply Newton’s second law in the horizontal direction. As the cylinder is rolling hence, torque will be acting on the cylinder. Balance the torques due to frictional force, the given force of $40N$ and the torque due to gravitational force. These torques will be responsible for the angular acceleration of the cylinder.

Complete step by step solution:
We are given with a hollow cylinder which has mass, $m = 5kg$
Radius of the hollow cylinder is given as, $R = 0.5m$
The horizontal force has magnitude, $F = 40N$
We have two forces acting in the horizontal direction; frictional force and the horizontal force.
Using Newton’s second law, we have:
$40 + f = ma$-------equation (1)
Here, $a$ is the linear acceleration of the cylinder
As the cylinder is rolling thus, torque is acting on the cylinder.
The horizontal force acting on the cylinder is providing torque in the clockwise direction. The frictional force acting at the bottom of the cylinder is providing torque in anticlockwise direction.
Both these torques are acting along the centre of the cylinder, as torque is given as a product of force with the distance from the axis of rotation. Thus, we have:
$R \times 40 - R \times f = I\alpha$
Here, $I$ is the moment of inertia of the cylinder such that $m{R^2}$
$\alpha$ is the angular acceleration of the cylinder, as the cylinder is rolling without slipping thus, we have $a = R\alpha$
Substituting these values in the above equation, we have:
$R \times 40 - R \times f = m{R^2}\alpha$
$\Rightarrow 40 - f = mR\alpha$------equation (2)
But from equation 1 we have
$40 + f = ma$
$\Rightarrow 40 + f = m\left( {R\alpha } \right)$ ----equation (3)
Adding equation 2 and equation 3 , we get
$80 = 2mR\alpha$
$\Rightarrow \alpha = \dfrac{{80}}{{2mR}}$
Substituting the values of $m = 5kg$ and $R = 0.5m$ we get
$\Rightarrow \alpha = \dfrac{{80}}{{2 \times 5 \times \left( {0.5} \right)}}$
$\Rightarrow \alpha = \dfrac{{80}}{5}$
$\therefore \alpha = 16\,rad\,{s^{ - 2}}$
This is the angular acceleration of the cylinder.
Therefore, option B is the correct option.

Note: Newton’s second law implies that the sum of all forces must be equal to mass multiplied by acceleration. In this problem, as the cylinder was rolling without slipping thus, the sum of torque acting on the cylinder must be equal to the moment of inertia of the cylinder along the axis multiplied by the angular acceleration of the cylinder. Torque due to gravity also acts on the cylinder but as gravitational force acts at the centre of mass of the cylinder thus the cross product of force and distance becomes zero since the angle between them is zero.