Question

A string is used to pull a block of mass m vertically up by a distance h at a constant acceleration$\dfrac{g}{3}$. The work done by the tension in the string is

& \text{A}\text{. }\dfrac{2}{3}mgh \\\ & \text{B}\text{. }\dfrac{-mgh}{3} \\\ & \text{C}\text{. }mgh \\\ & \text{D}\text{. }\dfrac{4}{3}mgh \\\ \end{aligned}$$

Answer 1

We have to find the work done by the tension in the string, for this first we can draw a diagram for the given question and then by balancing the forces we can find the tension in the string. Work done in terms of tension is given as a product of tension and the distance. Here distance is given as h and acceleration is given in terms of acceleration due to gravity.

Formula used:
$W=T\times d$

Complete answer:
Let us draw a diagram for the given question

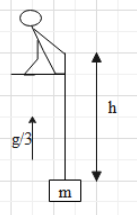
As we have to find tension in the string, then the forces acting on the string can be shown as

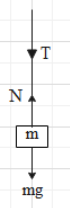
Here T is the tension in the string and N is the normal force acting upward whereas mg is the downward gravitational force. As the acceleration with which the string is pulled vertically upwards normal force N is given as
$N=m\dfrac{g}{3}$
Now balancing the forces in the string, we get the following equation

& T-m\dfrac{g}{3}=mg \\\ & \Rightarrow T=mg+\dfrac{mg}{3} \\\ & \Rightarrow T=\dfrac{4}{3}mg \\\ \end{aligned}$$ Now work done by the tension in the string is given as $$W=T\times h$$ Here h is the distance from which the object is pulled. Substituting value of tension we deduce above, we get $$W=\dfrac{4}{3}mgh$$ **Hence option D is correct.** **Note:** The unit of tension is Newton as it is the force experienced due to pulling or compressing a spring or string. Unit of tension is not mentioned to avoid confusion between normal force and newton as it is denoted by N. Similarly the unit of work is joules. While balancing the forces note that the forces applied in the same direction will be added whereas the forces in opposite directions are subtracted.