Question

A string $120cm$ in length sustains a standing wave, with the points of string at which the displacement of the amplitude is equal to $\sqrt 2 mm$ being separated by $15.0cm$.The maximum displacement amplitude is
A) $2mm$
B) $10mm$
C) $15mm$
D) $25mm$

Answer 1

A standing wave is a wave that does not travel or move. In a standing wave all the points will oscillate with equal and same amplitude along the string. The points at the end of the string do not oscillate and are called nodes. But the points those vibrate are known as anti nodes.

Complete step by step explanation:
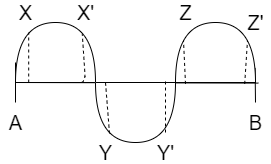
Step I: Let A and B be the end points of a string. Also suppose that XX’, YY’, ZZ’ are the amplitudes of the waves of the string. If $\lambda$ is the wavelength of the waves of the string, then the length of each wave will be
$l = \dfrac{{n\lambda }}{2}$---(i)
Where $n = 1,2,3,...$

Step II: The number of wavelengths in a given cycle of waves is described by its wave number. It is denoted by symbol k. It’s formula is
$k = \dfrac{{2\pi }}{\lambda }$
$\lambda = \dfrac{{2\pi }}{k}$---(ii)

Step III: Substitute the value of wavelength from equation (ii) to (i) and solve
$l = \dfrac{n}{2}(\dfrac{{2\pi }}{k})$
$l = \dfrac{{n\pi }}{k}$---(iii)

Step IV: Given that the waves are separated by a distance of $15.0cm$, so the distance between Z’ to X is
$\lambda = 4 \times 15 = 60cm$
Substituting the value in equation (i),
$120 = \dfrac{{n \times 60}}{2}$
$n = \dfrac{{240}}{{60}}$
$n = 4$

Step V: Substitute the value of n in equation (iii)
$120 = \dfrac{{4 \times \pi }}{k}$
$k = \dfrac{\pi }{{30}}$

Step VI: Amplitude of a stationary wave measures the strength or intensity of the waves. It is the maximum displacement of the waves. It is given by
$a = A\sin Kx\cos \omega t$
Where $A$is the amplitude
$x$is the displacement
$\omega$is the angular frequency
$t$is the time
At $t = 0$
$a = A\sin Kx$

Step VII:
Given $a = \sqrt 2 mm$
$K = \dfrac{{2\pi }}{\lambda } = \dfrac{{2\pi }}{{60}}$
$x = 7.5cm$
Substitute the values in the formula,
$\sqrt 2 = A\sin (\dfrac{{2\pi }}{{60}} \times 7.5)$
$\sqrt 2 = A\sin \dfrac{\pi }{4}$
$\sqrt 2 = \dfrac{A}{{\sqrt 2 }}$
$A = \sqrt 2 \times \sqrt 2$
$A = 2mm$

Step VIII: The maximum displacement amplitude is $2mm.$

Option (A) is the right answer.

Note: It is to be noted that the stationary wave is also known as standing wave. It is formed of a combination of two waves moving in opposite directions. The waves have the same amplitude and frequency. When waves superimpose then interference patterns occur and their energies either add or cancel out.