Question

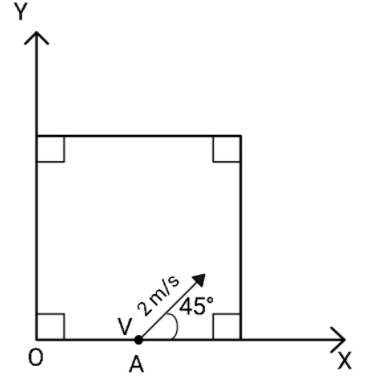
A striker is shot from a square carrom board from a point A exactly at the midpoint of one of the walls with a speed of 2 m/sec at an angle of $45^{\circ}$ with the axis as shown. The collisions of the striker with the walls of the fixed carrom are perfectly elastic. The coefficient of kinetic friction between the striker and the board is 0.2. The coordinate of the striker when it stops (taking point O to be the origin) is:

A. $\dfrac{1}{2 \sqrt{2}}, \dfrac{1}{ \sqrt{2}}$
B. $0, \dfrac{1}{2 \sqrt{2}}$
C. $\dfrac{1}{2 \sqrt{2}}, 0$
D. $\dfrac{1}{\sqrt{2}}, \dfrac{1}{2 \sqrt{2}}$

Answer 1

The friction due to the board creates retardation on the striker. Finding out this deceleration, will help us in finding the total (linear) distance the striker travels before coming to rest. Later, we can use simple geometry and see how the striker covers that distance and then we can find our required coordinates.

Formula used:
The linear distance traveled by the striker undergoing deceleration due to friction is:
$s = ut -\dfrac{1}{2}at^2$.

Complete answer:
In our case, the striker is undergoing an elastic collision so upon collision with the wall (which is and will always be at rest), the striker happens to merely change its direction. Therefore, the magnitude of the velocity remains the same but the direction slightly changes upon collision in absence of any external force upon the striker.
To simplify the logic, we can assume a scenario where the striker happens to be moving linearly only opposed by friction given as
$F = \mu mg$.
We can find out the magnitude of deceleration as:
$ma = \mu mg$ or $a = \mu g$.
We are given $\mu$ = 0.2 and taking g = 10 m/$s^2$ we can get:
$a = 2 ms^{-2}$.
We know from first law of motion:
v = u + at ;
0 = 2 - 2t ;
t = 1 s.
As v = 0 and a = -2 $ms^{-2}$ due to deceleration.
Now, using this and substituting the initial velocity as u = 2 m/s in the second law of motion, we get:
$s = 2 \times 1 - \dfrac{1}{2} \times 2 \times 1^2 = 1$m.

Therefore, the striker must cover a distance of 1 m before coming to rest.
Now, consider the geometry of the given carrom board.
The distance covered by the striker before it hits first wall (parallel to Y axis) is going to be:
$\sqrt{\dfrac{1}{(2 \sqrt{2})^2} + \dfrac{1}{(2 \sqrt{2})^2}} = \dfrac{1}{2}$m .
After this distance, it hits the wall and it is quite obvious that it moves towards the second wall (parallel to x-axis). This collision just reverses the x component of the velocity of the striker.
Therefore, the distance to the next wall is another 1/2 m.
So, it will be at the second wall along the motion of the striker, where the striker will finally come to rest after traveling (1/2 + 1/2 =) 1m distance.
The coordinates of the mid point of this second wall (upper wall) is our required answer. The y-coordinate is the length of the side of the square and x- coordinates is half of the length of the side.

Therefore, the required coordinates are $\left(\dfrac{1}{2 \sqrt{2}} , \dfrac{1}{\sqrt{2}}\right)$ which gives us the correct answer as option (A).

Note:
The case of a striker colliding with the wall can be assumed to be similar to a case when a small object collides with a much heavier object and gets reflected completely back. The motion of the striker can also be thought to be just like reflection of light when it falls at angle on a plane mirror.