Solveeit Logo
Login

Question

Question: A stretched string of length 1 m and mass \[5\times {{10}^{-4}}kg\], fixed at both ends, is under a ...

A stretched string of length 1 m and mass 5×10−4kg5\times {{10}^{-4}}kg, fixed at both ends, is under a tension of 20 N. If it is plucked at points situated at 25 cm from one end, it would vibrate with a frequency:
A. 400 Hz
B. 200 Hz
C. 100 Hz
D. 256 Hz

Explanation

Solution

The formula used to calculate the fundamental frequency of a string should be used to find the value of the frequency of the vibration of the plucked string. Lengths of the string and the plucked string are given in different units, so, change it accordingly.

Formula used: F=TMLF=\sqrt{\dfrac{T}{ML}}

Complete step by step answer:
From given, we have the data,
The length of the stretched string, L = 1 m
The mass of the stretched string, m = 5×10−4kg5\times {{10}^{-4}}kg
The tension in the stretched string, T = 20 N
The distance from the fixed end to antinode = 25 cm
Consider the formation of the node at the plucked string and even its vibration.

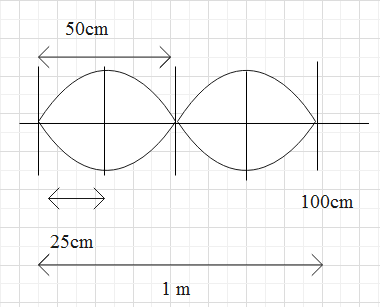
From the figure, it’s clear that the node formation takes place both the ends as they are closed and in the middle. Therefore, a total of 2 loops get formed each of length equal to 50 cm. Therefore, an antinode gets formed when the string is plucked at a distance of 25 cm.

The fundamental frequency of a loop formed will be equal to twice the fundamental frequency of the entire string.
Thus, the fundamental frequency becomes,
F=2×12LTLMF=2\times \dfrac{1}{2L}\sqrt{\dfrac{TL}{M}}
Upon rearranging the terms, we get the equation as follows.

& F=\sqrt{\dfrac{TL}{M{{L}^{2}}}} \\\ & \Rightarrow F=\sqrt{\dfrac{T}{ML}} \\\ \end{aligned}$$ Hence, the equation for the calculation of the frequency of the vibrations of the plucked string. Now, substitute the given values in the above equation to find the value of the frequency of the vibrations of the plucked string. $$\begin{aligned} & F=\sqrt{\dfrac{20}{5\times {{10}^{-4}}\times 1}} \\\ & \Rightarrow F=200\,Hz \\\ \end{aligned}$$ Thus, the value of the frequency of the vibrations of the plucked string. As the plucked string would vibrate with a frequency of 200 Hz **So, the correct answer is “Option ”.** **Note:** The things to be on your finger-tips for further information on solving these types of problems are: The units of the given parameters should be taken care of, as the length of the string is given in terms of meters and the same string is being plucked at a length of 25 cm.