Question

A street-light is hung $20\,ft$ above the ground. An object falls freely under gravity, starting from rest at the same height as the lamp and at a horizontal distance of $5\,ft$ from it. When the object has fallen through $16\,ft$ , the speed of the shadow of the object on the ground is:
A. $12\,ft{s^{ - 1}}$
B. $11\,ft{s^{ - 1}}$
C. $10\,ft{s^{ - 1}}$
D. $12.5\,ft{s^{ - 1}}$

Answer 1

Here first we have to assume the heights and distance and then we have to find the velocity of shadow by differentiating height and distance with respect to time. Here we have used a form of the third equation of motion to get the velocity of the object as $\sqrt {2gh}$. The real equation is ${v^2} = {u^2} + 2gh$, which is one of the uniformly accelerated motion equations. When $v =$final velocity,$u =$ initial velocity, $g =$ gravity and $h =$height acceleration. When $u = 0$ (for an object beginning from rest), the equation becomes ${v^2} = 2gh$ .

Complete step by step answer:
Let $H$ be the height of the street-lamp. Let $h$ be the height the object has fallen through.Let $D$ is the horizontal distance between the lamp and object.
Given, $H = 20\,ft$, $h = 16\,ft$, $D = 5\,ft$

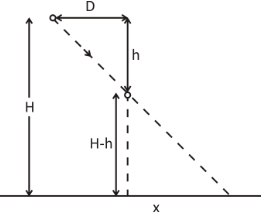
From the figure we get:
\dfrac{h}{D} = \dfrac{{H - h}}{x} \\\ \Rightarrow x = D \times \dfrac{{\left( {H - h} \right)}}{h} \\\ \Rightarrow x = D \times \left( {\dfrac{H}{h} - 1} \right) \\\
Let the velocity of shadow be $\dfrac{{dx}}{{dt}}$. Let the velocity of the object be $\dfrac{{dh}}{{dt}}$.
$\dfrac{{dx}}{{dt}} = D \times H \times \left( {\dfrac{{ - 1}}{{{h^2}}}} \right)\dfrac{{dh}}{{dt}}$
Velocity of shadow
V = 5 \times 20 \times \dfrac{1}{{{{16}^2}}} \times \sqrt {2gh} \\\ \Rightarrow V = 5 \times 20 \times \dfrac{1}{{{{16}^2}}} \times \sqrt {2 \times 32 \times 16} \\\ \therefore V = 12.5\,ft{s^{ - 1}} \\\
Hence, option D is the answer.

Additional information:
In physics, equations of motion are classified as equations that characterise a physical system’s behaviour in terms of its motion as a function of time. For deriving components such as displacement, velocity, time and acceleration, there are three motion equations that can be used.

Acceleration is known to be used as a term for speeding up and deceleration for speeding down. However, speeding up may be referred to as positive acceleration and slowing down as negative acceleration.

The average velocity of the object is the total displacement of the object divided by the total time taken. In other words, the pace at which an object changes its location from one place to another. Average velocity is a quantity of vectors. The SI unit is one metre per second.

Note: Here we have to remember that the units are in feet. So, while calculating the velocity, the acceleration due to gravity should be converted to feet per second square, otherwise the answer would be wrong. The sum of the original and final velocity is separated by $2$ velocity equal to the sum of the final velocity and the original velocity over $2$.