Question

A street light is 6 m high. A man 180 cm tall goes away from the street light at a speed of 120 cm/sec. Find the rate of increase of length of his shadow when he is 9 m away from the light. Also find the rate at which the tip of the shadow moves on the road.

Answer 1

We will use the similarity of triangles to solve this question. We will also use differentiation to find the rate at which shadow moves. The speed of an object is found using the formula speed = distance/time. We will use this formula to solve the given question.

Complete step-by-step answer:
Now, we will first draw a figure according to the question.

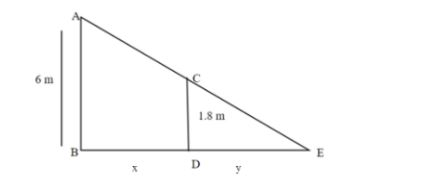
Now, in this figure AB represents the street light which is 6 m high. The CD represents the man 1.8 m or 180 cm tall. BD is the distance of the man from the street light and DE is the length of shadow of the man. Let BD be x and DE be y.
Now, by using similarity of triangles, in $\Delta ABE$ and $\Delta CDE$, we have
$\angle AEB = \angle CED$ (Common)
$\angle ABE = \angle CDE = 90^\circ$
So, by AA similarity, we get $\Delta ABE \sim \Delta CDE$
So, we can write, $\dfrac{{AB}}{{CD}} = \dfrac{{BE}}{{DE}}$
Now, BE = BD +DE,
So, we have $\dfrac{6}{{1.8}} = \dfrac{{x + y}}{y}$,
$\dfrac{{10}}{3} = \dfrac{{x + y}}{y}$
So, we get $y = \dfrac{3}{7}x$ … (1)
Now, the speed at which man is moving away from the light is 120 cm/sec.
Also, speed of man moving away from street light = $\dfrac{{dx}}{{dt}}$
Therefore, $\dfrac{{dx}}{{dt}}$ = 120 cm/sec
Now, to get the rate at which tip of shadow is moving, we will differentiate equation (1) with respect to t.
So, the rate at which the tip of shadow is moving = $\dfrac{{dy}}{{dt}} = \dfrac{{d\left( {\dfrac{3}{7}x} \right)}}{{dt}}$ = $\dfrac{3}{7}(120)$ = $\dfrac{{360}}{7}$ cm/sec
So, we get, $\dfrac{{dy}}{{dt}} = \dfrac{{360}}{7}$ cm/sec.
Now, we can see that $\dfrac{{dy}}{{dt}}$ is independent of x, so the rate of increase of length is constant.

Note: Whenever we come up with such types of questions, we will first draw a diagram according to the question. Then, we will assume variables x and y as distance of man from street light and distance of shadow from street light. Then, we will use the property of similarity which states that if two triangles are similar then, their corresponding sides are in the same ratio or proportion. To find the rate at which any object moves we use the technique of differentiation. Like in this question, we first use similarity to find a relation between the distance between man and street light and length of shadow. After it, we use the technique of differentiation to find the rate at which the tip of the shadow is moving.