Question
Question: A straight wire of finite length carrying current I subtend an angle of \[60^\circ \] at point P as ...
A straight wire of finite length carrying current I subtend an angle of 60∘ at point P as shown. The magnetic field at P is:
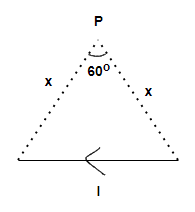
A) 23πxμ0I
B) 2πxμ0I
C) 2πx3μ0I
D) 33πxμ0I
Solution
This given problem can be solved by taking the consideration of the magnetic field due to finite long straight wire carrying current I throughout the wire.
Complete step by step solution:
Step 1: As it is given in the question a straight wire of finite length carrying current I subtend an angle of 60∘ at point P.
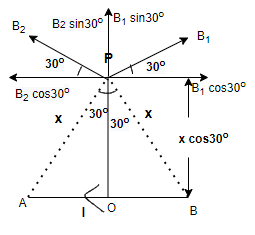
As shown in above figure, the magnetic field at point P will be the total magnetic field produced by point A and point B.
We can calculate the length PO by taking the consideration of right angle triangle and trigonometric angles such as cosθ=Adjacent/ hypotenuse
So, cosθ=APPO
PO=APcosθ (1)
Where, AP=x and θ=30∘
After keeping all the values in above equation (1), we will get –
PO=xcos30∘ (2)
Step 2: Now, we have to calculate the magnetic field due to a straight current carrying conductor of finite length at a point P, perpendicular distance PO from the linear conductor AB is given by –
B=4πμ0POI(sinϕ1+sinϕ2) (3)
Where, ϕ1=ϕ2=30∘ and PO=xcos30∘
So, after keeping the all values in above equation (3), we will get –
B=4πμ0xcos30∘I(sin30∘+sin30∘) on further solving this equation
B=4πμ0xcos30∘I(2sin30∘)
B=4πμ0xcos30∘I(2sin30∘) on further simplifying this equation
B=4πμ0xI2tan30∘ as we know that tan30∘=31 so keeping this value in the equation
B=2πμ0xI31 on rearranging this equation
B=23πμ0xI
So, the magnetic field at point P will be B=23πμ0xI.
So, the correct option is (A).
Note:
(i) As current is flowing in the conductor from B to A, the direction of magnetic field is normal to the plane of conductor downwards.
(ii) If the direction is opposite i.e. from the A to B, then the direction of the magnetic field is normal to the plane of conductor upwards.
