Question

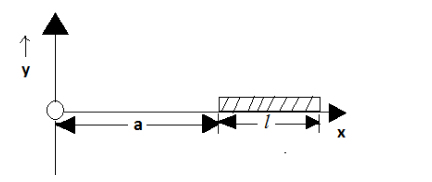
A straight rod of length $l$ extends from $x = a$ to $x = l + a$ . If the mass per unit length is $\left( {a + b{x^2}} \right)$ , the gravitational force it exerts on a point mass $m$ placed at $x = 0$ is given by:

\left( A \right)Gml\left( {b + \dfrac{a}{{a\left( {l + a} \right)}}} \right) \\\ \left( B \right)\dfrac{{Gm}}{{l\left( {l + a} \right)}}\left\\{ {a\left( {l + a} \right) + b{l^3}} \right\\} \\\ \left( C \right)Gml\left( {bl + \dfrac{a}{{l + a}}} \right) \\\ \left( D \right)Gm\left\\{ {b\left( {l + a} \right) + \dfrac{a}{l}} \right\\} \\\

Answer 1

In order to solve this question, we are going to first take the mass per unit length of the rod, from that the length corresponding to a small mass element is found that length gives an ease to find the gravitational force for that small mass and length and then, the force is integrated from limits $x = a$ to $x = l + a$ .
The force $dF$ that is exerted on the mass $dm$ due to gravitational field,
$dF = \dfrac{{GMdm}}{{{x^2}}}$

Complete step by step solution:
As it is given in the question that the straight rod of length $l$ extends from $x = a$ to $x = l + a$
Now the mass per unit length is given in terms of $\left( {a + b{x^2}} \right)$ , thus the small change in mass $dm$ corresponding to the small change $dx$ in the length of the rod can be expressed as
$dm = \left( {a + b{x^2}} \right)dx$
The force $dF$ that is exerted on the mass $dm$ due to gravitational field,
$dF = \dfrac{{GMdm}}{{{x^2}}}$
On integrating the force from the limits from which length is extending, i.e. , $x = a$ to $x = l + a$
$F = \int\limits_a^{a + l} {\dfrac{{GMdm}}{{{x^2}}}}$
Putting $dm$ equals $\left( {a + b{x^2}} \right)$ ,
F = \int\limits_a^{a + l} {\dfrac{{GM\left( {a + b{x^2}} \right)dx}}{{{x^2}}}} \\\ \Rightarrow F = \int\limits_a^{a + l} {\left( {\dfrac{{GMa}}{{{x^2}}} + GMb} \right)} dx \\\ \Rightarrow F = - GMa{\left. {\dfrac{1}{x}} \right|_{x = a}}^{x = a + l} + {\left. {GMbx} \right|_{x = a}}^{x = a + l} \\\ \Rightarrow F = - GMa\left( {\dfrac{1}{{a + l}} - \dfrac{1}{a}} \right) + GMb\left( {a + l - a} \right) \\\ \Rightarrow F = GMa\left( {\dfrac{l}{{\left( {a + l} \right)a}}} \right) + GMb\left( l \right) \\\ \Rightarrow F = GMl\left[ {b + \dfrac{1}{{a + l}}} \right] \\\
Now, further simplifying the relation obtained above in order to match according to the options, we get
$F = GMl\left[ {b + \dfrac{a}{{a\left( {a + l} \right)}}} \right]$
Hence, the option $\left( A \right)Gml\left( {b + \dfrac{a}{{a\left( {l + a} \right)}}} \right)$ Is the correct answer.

Note:
The fact that the mass per unit length is given in the question gives us the right to take any infinitesimally small mass element out of the rod and find out the corresponding length for it as we are given the mass per unit length after which, the gravitational force for that small mass element is calculated.