Question

A straight pillar PQ stands at a point P, the points A and B are situated due south and east of P respectively. M is the midpoint of AB. PAM is an equilateral triangle and N is the foot of the perpendicular from P on Ab. Suppose AN $= 20$ metre and the angle of elevation of the top of the pillar at N is ${\tan ^{ - 1}}2.$ Find the height of the pillar and the angles of elevation of its top at A and B.

Answer 1

Hint : The upwards angle from the horizontal axis from the observer to the point of interest is known as the angle of elevation. With the help of the given conditions draw the perfect diagram and apply trigonometric functions accordingly. Here, we will use tangent function since we are given the measures of the opposite and the adjacent sides.

Complete step-by-step answer :

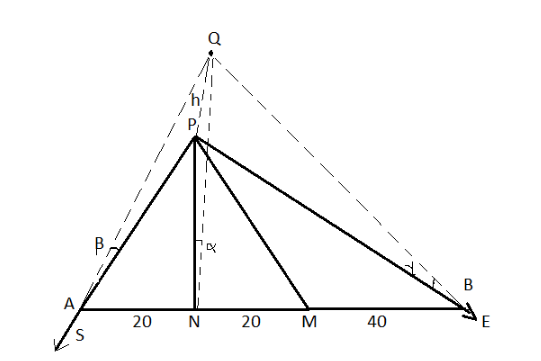
Let us assume that PQ is the vertical pillar.
The point A and the point B are respectively due south and due east of the point P such that $\angle APB = 90^\circ$ where M is the mid-point of the AB and N is the base of the perpendicular from P on AB.
Also, given that AN $= 20\,{\text{metres}}$
In $\Delta PAM$ is an equilateral triangle where N is the mid-point of AM.
$\therefore AM = 2AN = 40\;{\text{ }}....{\text{ (i)}}$
Similarly, $AB = 2AM = 80\;{\text{ }}....{\text{ (ii)}}$
In $\Delta PAM$ is an equilateral triangle, all the angles in the triangle $= 60^\circ$
$\Rightarrow \angle PAM = \angle MPA = 60^\circ$
Where $\tan \alpha = 2$
Let us assume that $PQ = h$
Then, by using the trigonometric concepts-
$PN = h\cot \alpha = AN\tan 60^\circ$
Place the values in the above equation – using the property that cot and tan function are inverse to one another, Where $\tan \alpha = 2$
$\Rightarrow h\left( {\dfrac{1}{2}} \right) = 20\sqrt 3$
When the term in division changes its side, then it goes to the multiplicative on the opposite side.
$\Rightarrow h = 20 \times 2\sqrt 3 = 40\sqrt 3$ ..... (iii)
Now, find the elevation of A and B,
$\Delta PAM$ is an equilateral triangle, $PA = AM = 40$
By using the equations (i) and (ii)
$\therefore PB = \sqrt {A{B^2} - P{A^2}}$
Place the values –
$\therefore PB = \sqrt {{{80}^2} - {{40}^2}}$
Simplify the above equation –
$\therefore PB = \sqrt {6400 - 1600} \\\ \therefore PB = \sqrt {4800} \\\ \therefore PB = \sqrt {1600 \times 3} \\\ \therefore PB = 40\sqrt 3 {\text{ metres}} \;$
Use tangent function as the ratio of the opposite side with the adjacent side.
$\Rightarrow \tan \beta = \dfrac{{PQ}}{{PA}}$
Place the values-
$\Rightarrow \tan \beta = \dfrac{{40\sqrt 3 }}{{40}}$
Common multiple from the numerator and the denominator cancel each other.
$\Rightarrow \tan \beta = \sqrt 3 \\\ \Rightarrow \beta = {\tan ^{ - 1}}\sqrt 3 \\\ \Rightarrow \beta = 60^\circ \;$
Similarly,
$\Rightarrow \tan \gamma = \dfrac{{PQ}}{{PB}}$
Place the values-
$\Rightarrow \tan \gamma = \dfrac{{40\sqrt 3 }}{{40\sqrt 3 }}$
Common multiple from the numerator and the denominator cancel each other.

$$\Rightarrow \tan \gamma = 1 \\\ \Rightarrow \gamma = {\tan ^{ - 1}}1 \\\ \Rightarrow \gamma = 45^\circ \;$$

Note : Know the difference between the angle of elevation and the angle of depression and apply accordingly. Draw the diagram properly with the given conditions then rest goes well. Please remember all the different trigonometric angles which are the angles given by the ratios of the trigonometric functions. The most important trigonometric angles are $0^\circ ,{\text{ 3}}0^\circ ,\;45^\circ ,{\text{ 6}}0^\circ {\text{ and 9}}0^\circ$ . Remember the values of these angles for quick substitution for further simplification.