Question

A straight metal rod of length 3l is bent through the right angle as shown. The bent rod is then placed on a rough horizontal table. A light string is attached to the vertex of the right angle. The string is then pulled horizontally so that the rod slides at a constant velocity. Find the angle α that slide 2l would make with the string.

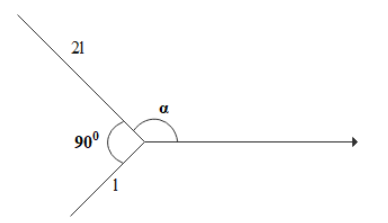
A. ${166^0}$
B. ${156^0}$
C. ${14^0}$
D. ${24^0}$

Answer 1

When a body is in equilibrium that means body will be in both rotational equilibrium and translational equilibrium. Which means all the forces will be balanced and the net torque about any point will be zero. We take the point of our convenience and find out the torque about that point and equate it to zero to solve this.

Formula used:
${\rm T} = \mathop r\limits^ \to \times \mathop F\limits^ \to$

Complete answer:
It is given that the rod is uniform which means mass will be uniformly distributed. If the mass of the part whose length is ‘l’ is ‘m’ then the mass of the part whose length is ‘2l’ will be ‘2m’. The word rough is used in the question to give us a hint that the table has a friction. Hence it is clear that if it has a friction then if the rod of length ‘l’ experiences friction force ‘f’ then the rod of length ‘2l’ experiences force ‘2f’ because frictional force will be dependent on mass.

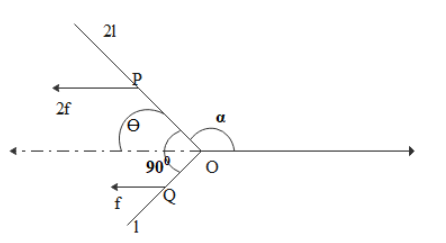
Now those two frictional forces will act horizontally at the center of masses of the two rods. Center of mass of the rod lies exactly at its geometrical center as the rod is uniform. Let P and Q be the center of masses of bigger portion and the smaller portion respectively. O be the joint where two portions meet. So $OP = l,OQ = \dfrac{l}{2}$. Let $\theta$ be the angle made by the bigger portion with the horizontal.
We will equate the torque produced by two frictional forces about ‘O’ to zero to get the answer.
We have torque as ${\rm T} = \mathop r\limits^ \to \times \mathop F\limits^ \to$ where its magnitude will be ${\rm T} = rF\sin \theta$ where $\theta$ is the angle between force and the position vector with respect to the point where torque is to be found.
Torque created due to ‘2f’ frictional force about joint ‘O’ is $2fl\sin \theta$
Torque created due to ‘f’ frictional force about the joint ‘O’ is $- \dfrac{{fl\cos \theta }}{2}$ where negative sign indicates this is in the opposite direction to the previous torque.
Equate net torque to zero
$\Rightarrow 2fl\sin \theta - \dfrac{{fl\cos \theta }}{2} = 0$
\eqalign{ & \Rightarrow \dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{1}{4} \cr & \Rightarrow \tan \theta = \dfrac{1}{4} \cr & \Rightarrow \theta = \arctan (\dfrac{1}{4}) \cr & \Rightarrow \theta = {14^0} \cr & \Rightarrow \alpha = 180 - \theta \cr & \Rightarrow \alpha = 180 - {14^0} \cr & \Rightarrow \alpha = {166^0} \cr & \cr}

Hence answer would be option A.

Note:
Body is moving with constant velocity means it is in equilibrium or else there will be change in velocity. The other thing to be noted is that the tension in the string is not known to us. So to avoid it we considered torque about joint ‘O’ because about that point string doesn’t produce any torque.