Question

A straight line through the point $A(3,4)$ is such that its intercept between the axes is bisected at A. it’s equation is-
A. $3x - 4y + 7 = 0$
B. $4x+ 3y = 24$
C. $3x - 4y = 25$
D. $x - y = 7$

Answer 1

Hint : In this question, the point $A(3,4)$ which passes through the straight line. To find the equation of line, we use the slope-intercept formula. First we determine the end point of the straight line and evaluate by using the formula.

Complete step-by-step answer :
Here $A(3,4)$ is a point which passes through the straight line. Consider $BC$ is a straight-line having points $(a,0)$ and $(0,b)$ . Let $A$ be the midpoint of the line $BC$ .

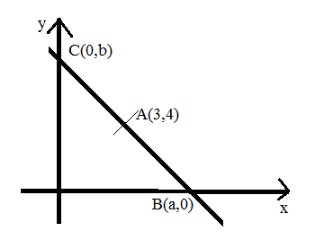
By using the midpoint formula, we determine the end points as

$$\dfrac{{a + 0}}{2} = 3{\text{ and }}\dfrac{{0 + b}}{2} = 4 \\\ \Rightarrow \dfrac{a}{2} = 3{\text{ and }}\dfrac{b}{2} = 4 \;$$

By simplifying, we have $a = 6$ and $b = 8$ .
Hence, we determined the endpoints. Now we have to find the equation of line.
To find the equation of line we consider the slope-intercept formula which is given by $y = mx + b$ . $y$ is $y$ coordinate, $m$ is slope, $x$ is $x$ coordinate and $b$ is $y$ intercept.
First we determine the slope $m$ is given by $m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$ where $({x_1},{y_1})$ and $({x_2},{y_2})$ are the endpoints of the straight line. Here $({x_1},{y_1})$ and $({x_2},{y_2})$ are $(6,0)$ and $(0,8)$

$$m = \dfrac{{8 - 0}}{{0 - 6}} \\\ = \dfrac{8}{{ - 6}} = - \dfrac{8}{6} \;$$

Therefore the equation of line by intercept formula is $y = mx + b$
$y = \left( { - \dfrac{8}{6}} \right)x + 8$
By taking L.C.M.

$$y = \dfrac{{ - 8x + 48}}{6} \\\ \Rightarrow 6y = - 8x + 48 \;$$

Dividing the above equation by 2 we have

$$3y = - 4x + 24 \\\ \Rightarrow 4x + 3y = 24 \;$$

∴ the equation of line is given by $4x + 3y = 24$
So, the correct answer is “Option B”.

Note : To find the equation of a line we need the end points. In this question first, we have to determine the endpoints of the straight line. After determining the endpoints, we can determine the equation of the line by using the slope intercept formula. Here we considered the point $A(3,4)$ as midpoint and we determined the end points and evaluated them using the slope intercept formula.