Question

A straight line through the origin O meets the parallel lines 4x + 2y = 9 and 2x + y + 6 = 0 at points P and Q respectively. Then what is the ratio in which the point O divides the segment PQ?
(a). 1:2
(b). 3:4
(c). 2:1
(d). 4:3

Answer 1

Hint: By the intercepts theorem, all the intercepts to the lines 4x + 2y = 9 and 2x + y + 6 = 0 and passing through the origin are divided in the same ratio. Use this to assume a simple intercept and find the ratio.

Complete step-by-step answer:
The intercept theorem is about the ratio of line segments. If there are two parallel lines and there are two intercepts passing through a point S, one cutting the parallel lines at A and B and the other cutting the line at C and D, then the ratio of the line segments AS and BS is equal to the ratio of line segments CS and DS.
$\dfrac{{SA}}{{SB}} = \dfrac{{SC}}{{SD}}$
Using this, we can find the ratio in which the origin O divides the line segment PQ.
Let us consider another intercept between the line as the y-axis, which is x = 0.
The points at which the y-axis intersects the line 4x + 2y = 9 is given as below:
$4(0) + 2y = 9$
$2y = 9$
$y = \dfrac{9}{2}$
Hence, the point is $\left( {0,\dfrac{9}{2}} \right)$.
The points at which the y-axis intersects the line 2x + y + 6 = 0 is given as below:
$2(0) + y + 6 = 0$
$y = - 6$
Hence, the point is (0, - 6).

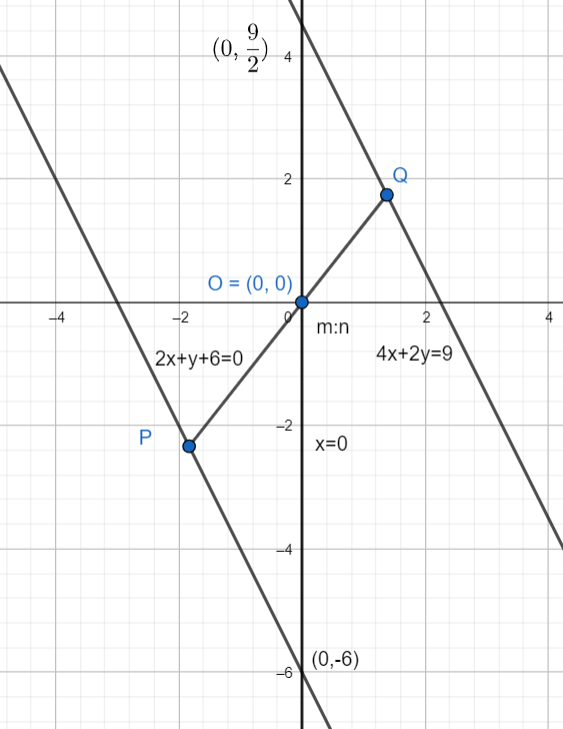
Now, the section formula for the line segment joining points $({x_1},{y_1})$ and $({x_2},{y_2})$ divided by the point (x, y) in the ratio m:n is given as follows:
$(x,y) = \left( {\dfrac{{m{x_2} + n{x_1}}}{{m + n}},\dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right)$
The ratio m:n in which the point (0, 0) divides the line segment joining $\left( {0,\dfrac{9}{2}} \right)$ and (0, - 6) is given as follows:
$(0,0) = \left( {\dfrac{{m(0) + n(0)}}{{m + n}},\dfrac{{m( - 6) + n\left( {\dfrac{9}{2}} \right)}}{{m + n}}} \right)$
Simplifying, we have:
$(0,0) = \left( {0,\dfrac{{ - 6m + \dfrac{9}{2}n}}{{m + n}}} \right)$
The corresponding coordinates should be equal. Hence, we have
$\dfrac{{ - 6m + \dfrac{9}{2}n}}{{m + n}} = 0$
Simplifying, we have:
$- 6m + \dfrac{9}{2}n = 0$
$\dfrac{9}{2}n = 6m$
$\dfrac{m}{n} = \dfrac{9}{{2 \times 6}}$
$\dfrac{m}{n} = \dfrac{3}{4}$
Hence, by intercepts theorem, the origin divides the line segment PQ in the ratio 3:4.
Hence, the correct answer is option (b).

Note: You can also choose the x-axis to find the ratio in which the origin divides the line segment PQ. In this case, you have the equation y = 0 and you can proceed further.