Question
Question: A straight line through origin O meets the parallel lines \(4x+2y=9\) and \(2x+y+6=0\) at point P an...
A straight line through origin O meets the parallel lines 4x+2y=9 and 2x+y+6=0 at point P and Q respectively. Then the point O divides the segment PQ in the ratio.
a)1:2b)3:4c)2:1d)4:3
Solution
Now we are given that a straight line through origin O meets the parallel lines 4x+2y=9 and 2x+y+6=0 at point P and Q respectively. We know that equation of line passing through origin is in y=mx hence we will use this equation to solve with both lines to get the coordinates P and Q. Now we have coordinates of P, Q and O. hence we can use section formula which says if (x, y) divides the line joining (x1,x2) and (y1,y2) in ration m : n. then we have.
(x,y)=((m+nmx1+nx2),(m+nmy1+ny2)) . hence we can find the ratio m : n.
Complete step-by-step answer :
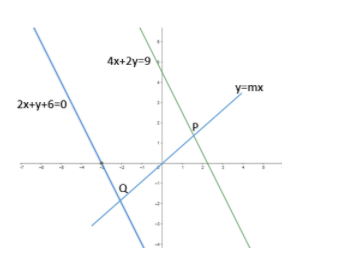
Now consider the equation of line passing through origin
We know that the equation of line passing through origin is y=mx
Now let us say the equation of line PQ is y=mx
Now Let us first find the point of intersection P.
P lies on line 4x+2y=9 and the line y=mx
Now consider the line 4x+2y=9
Dividing throughout by 2 we get
2x+y=29
Hence we get y=29−2x
Now at intersection point of line 4x+2y=9 and the line y=mx which is P we have
