Question

A straight line parallel to the line $2x-y+5=0$ is also a tangent to the curve ${{y}^{2}}=4x+5$ . Then, the point of contact is
A.(2,1)
B.(-1,1)
C.(1,3)
D.(3,4)
E.(-1,2)

Answer 1

Hint: To solve the question, we have to apply the properties of parallel lines to calculate the tangent line. Thus, the parallel line and the curve have a common point. To calculate the point, apply the formula of slope of line.

Complete step-by-step answer:

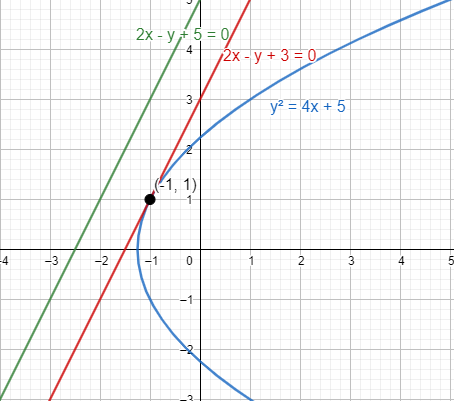
We know that the line parallel to the line $ax+by+c=0$ is $ax+by+d=0$.
Thus, the line parallel to the line $2x-y+5=0$ is $2x-y+d=0$
Thus, the line $2x-y+d=0$ is tangent to the curve ${{y}^{2}}=4x+5$ .
We know that the slope of line $ax+by+c=0$ is equal to $\dfrac{-a}{b}$
On comparing the general equation of line and he tangent line, we get
a = 2, b = -1, c = d
Thus, the slope of line $2x-y+d=0$ is equal to $\dfrac{-2}{-1}=2$ ….. (1)
The slope of tangent to the curve is given by the derivative of the curve.
Thus, we get
$\dfrac{d\left( {{y}^{2}} \right)}{dx}=\dfrac{d\left( 4x+5 \right)}{dx}$
We know the formula $\dfrac{d\left( {{x}^{n}} \right)}{dx}=n{{x}^{n-1}},\dfrac{d\left( cf(x) \right)}{dx}=c\dfrac{d\left( f(x) \right)}{dx},\dfrac{dc}{dx}=0$ where c is a constant.
By substituting the above formulae, we get
$2y\dfrac{dy}{dx}=4\dfrac{dx}{dx}+0$
$2y\dfrac{dy}{dx}=4$
$\dfrac{dy}{dx}=\dfrac{4}{2y}=\dfrac{2}{y}$
Thus, the slope of tangent to the curve is equal to $\dfrac{2}{y}$
From equation (1) we get
$\Rightarrow 2=\dfrac{2}{y}$
$y=\dfrac{2}{2}=1$
Thus, the value of y = 1
Since the point of contact lie on the curve, on substituting the above value of y we get
${{1}^{2}}=4x+5$
$1=4x+5$
$1-5=4x$
$-4=4x$
$x=\dfrac{-4}{4}=-1$
Thus, the point of contact of the tangent line and the given curve is (-1,1)
Hence, option (d) is the right choice.

Note: The problem of mistake can be not analysing that the slope of the tangent line is equal to slope of the tangent to the curve. The other possibility of mistake is not being able to apply the formula of differentiation to solve.