Question

A straight line meets the coordinate axes in A and B. Find the equation of the straight line, when $\overline{AB}$ is divided in the ratio 2 : 3 at (─5, 2).

Answer 1

To find the equation of the line, we need to find at least 2 points. It is given that the line intersects the axes in A and B. Suppose it intersects y – axis at point A and it intersects x – axis at point B. This means x – coordinate of A is 0 and y – coordinate of B is 0. Now, it is given that (─5,3) divides the line formed by A and B in the ratio 2 : 3. Here, we will use the section formula to find the point A and B. Once we’ve found A and B, we will use these points to form the equation of line.

Complete step by step answer:
Let the x – coordinate of point A be x and y – coordinate of point B be y.
Therefore, point B is (0, y) and point A is (x, 0),
If the point (─5, 2) divides the line, it must also lie on the line.
The figure of the line is as follows:

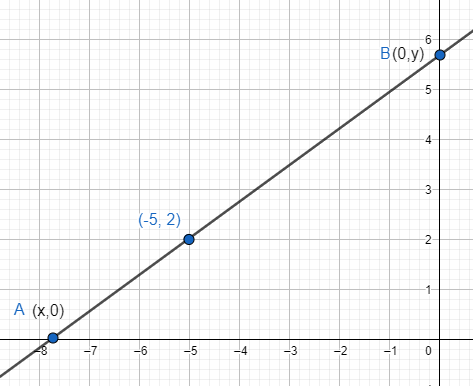
We will use the section formula to find the value of x and y.
The section formula is $\left( x,y \right)=\left( \dfrac{n{{x}_{1}}+m{{x}_{2}}}{m+n},\dfrac{n{{y}_{1}}+m{{y}_{2}}}{m+n} \right)$, where m : n is the ratio in which the point (x, y) divides point $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$.
The point (─5, 2) divides the line segment between A(x,0) and B(0,y) in the ration 2 : 3.
$\begin{aligned} & \Rightarrow \left( -5,2 \right)=\left( \dfrac{2x}{5},\dfrac{3y}{5} \right) \\\ & \Rightarrow -5=\dfrac{2x}{5},\ 2=\dfrac{3y}{5} \\\ & \Rightarrow x=\dfrac{-25}{2},\ y=\dfrac{10}{3} \\\ \end{aligned}$
Therefore, point coordinates of point A is $\left( \dfrac{-25}{2},0 \right)$ and that of point B is $\left( 0,\dfrac{10}{3} \right)$.
Thus, we find an equation of line passing through the points A and B.
Equation of line in two-point form is $y-{{y}_{1}}=\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)\left( x-{{x}_{1}} \right)$
$\begin{aligned} & \Rightarrow y-0=\left( \dfrac{\dfrac{10}{3}-0}{0-\left( -\dfrac{25}{2} \right)} \right)\left( x-\left( -\dfrac{25}{2} \right) \right) \\\ & \Rightarrow y=\left( \dfrac{\dfrac{10}{3}}{\dfrac{25}{2}} \right)\left( x+\dfrac{25}{2} \right) \\\ & \Rightarrow y=\dfrac{4}{15}\left( x+\dfrac{25}{2} \right) \\\ & \Rightarrow y=\dfrac{4}{15}x+\dfrac{10}{3} \\\ \end{aligned}$
Therefore, the equation of the line passing through A and B is $y=\dfrac{4}{15}x+\dfrac{10}{3}$

Note: Alternatively, students can find first find the slope of the line by the formula $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ and then find the equation of the line is slope-point form $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$.