Question

A straight highway leads to the foot of the tower, a man standing at the top of the tower observes a car at an angle of depression of ${30^ \circ }$ which is approaching the foot of the tower with uniform speed. Six seconds later, the angle of depression of the car is found to be ${60^ \circ }$. Find the time taken by the car to reach the foot of the tower from this point.

Answer 1

Draw the diagram of the scenario according to the conditions given in the questions. Formulate the equation between the distance travelled by the car and the distance left between the car and the tower by using the trigonometric ratios. Formulate equation relating the speed of the car and the distance travelled by the car using the formula ${\text{speed = }}\dfrac{{{\text{distance}}}}{{{\text{time}}}}$. Solve the equations formed to find the time required for the car to reach the tower.

Complete step-by-step answer:
Let us assume the height of the tower be $h$ meters.
Let us draw the figure according to the condition given in the question.

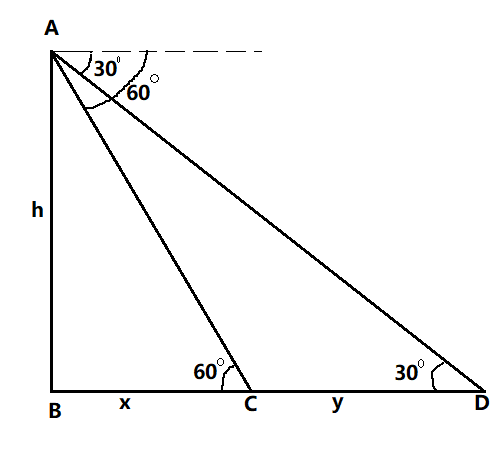
Here AB represents the tower, the point D represents the initial position of the car, and point C represents the position of the car after 6 seconds. It is known that in a right angled triangle, the $\tan \theta$ is given by the $\dfrac{{Opposite}}{{Base}}$.
For the triangle ABC, we can say that
$\tan {60^ \circ } = \dfrac{h}{x} \\\ \Rightarrow \sqrt 3 = \dfrac{h}{x} \\\ \Rightarrow h = \sqrt 3 x \\\$
Similarly, for the triangle ABD, we get
$\tan {30^ \circ } = \dfrac{h}{{x + y}} \\\ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{x + y}} \\\ \Rightarrow \sqrt 3 h = x + y \\\$
Substituting the value $\sqrt 3 x$ for $h$ in the equation $\sqrt 3 h = x + y$, we get
$\sqrt 3 \left( {\sqrt 3 x} \right) = x + y \\\ \Rightarrow 3x = x + y \\\ \Rightarrow 2x = y \\\$
Let us assume the speed of the car is $v$ m/sec.
It is given that the car took 6 seconds to reach from point D to point C. The distance travelled during the 6 seconds is represented by $y$.
Thus substituting $v$ for speed, $y$ for distance and 6 for time in the formula ${\text{speed = }}\dfrac{{{\text{distance}}}}{{{\text{time}}}}$, we get
$v = \dfrac{y}{6} \\\ \Rightarrow y = 6v \\\$
Substituting the value $6v$ for $y$ in the equation $2x = y$, we get
$2x = 6v \\\ \Rightarrow \dfrac{x}{v} = 3 \\\$
Let us assume the time required for the car to reach the foot of the tower from the point C is $t$ second.
substituting $v$ for speed, $x$ for distance and $t$ for time in the formula ${\text{speed = }}\dfrac{{{\text{distance}}}}{{{\text{time}}}}$, we get
$v = \dfrac{x}{t} \\\ \Rightarrow t = \dfrac{x}{v} \\\$
Substituting the value 3 for $\dfrac{x}{v}$ in the above equation, we get
$t = 3$
Thus the time taken by the car to reach from the point C to the foot of the tower is 3 seconds.

Note: The angle of depression is the angle made by the horizontal line of sight from the observer with some observational point below the horizontal line of sight. Here the angles $\angle ADB = {30^ \circ }$ and $\angle ACB = {60^ \circ }$ by the property of corresponding angles of the triangle.