Question

A straight highway leads to the foot of a tower to height$50m$. From the top of the tower, the angles of depression of two cars standing on the highway are ${30^0}$and ${60^0}$. What is the distance between the two cars and how far is each car from the tower?
${\text{A}}{\text{. 22}}{\text{.31 m, 28}}{\text{.86 m, 86}}{\text{.60 m}} \\\ {\text{B}}{\text{. 522}}{\text{.31 m, 35}}{\text{.24 m, 86}}{\text{.60 m}} \\\ {\text{C}}{\text{. 57}}{\text{.3 m, 35}}{\text{.24 m, 40}}{\text{.19 m}} \\\ {\text{D}}{\text{. None of these}} \\\$

Answer 1

“In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides”, this is the Pythagoras theorem. The sides of this triangle have been named as Perpendicular, Base and Hypotenuse. Here, the hypotenuse is the longest side, as it is opposite to the angle $90^\circ .$
Approaching by diagram use of Pythagoras theorem: ${H^2} = {B^2} + {P^2}$
Substituting$H = L$,$B = A$and $P = K$, we have:

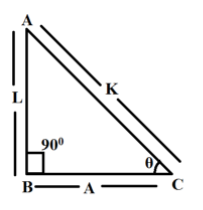
${L^2} + {A^2} = {K^2}$ and by trigonometric ratios:
$\sin \theta = \dfrac{L}{K}$; $\cos \theta = \dfrac{A}{K}$; $\tan \theta = \dfrac{L}{K}$

Complete step-by -step solution:
Give the tower of height $= 50m$
Angles of depression of two cars standing on the highway are ${30^0}$ and ${60^0}$.

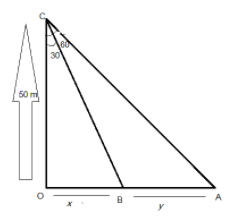
Consider the distance between the cars be y, and the distance of the car B from the tower be x.
Now use of Pythagoras theorem in $\vartriangle OBC$ as:

$$\Rightarrow \tan 30 = \dfrac{{OB}}{{0C}} \\\ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{x}{{50}} \\\ \Rightarrow x = \dfrac{{50}}{{\sqrt 3 }} \\\ = 28.86{\text{ meters}} \\\$$

Again, in $\vartriangle OAC$:

$$\Rightarrow \tan 60 = \dfrac{{OA}}{{OC}} \\\ \Rightarrow \sqrt 3 = \dfrac{{x + y}}{{50}} \\\ \Rightarrow 28.86 + y = 50 \times 1.732 \\\ \Rightarrow y = 86.6 - 28.86 \\\ = 57.74{\text{ meters}} \\\$$

Now, add x and y, to evaluate the distance between the tower and car A as:
$\Rightarrow x + y = 28.86 + 57.74 \\\ = 86.6{\text{ meters}} \\\$
Hence, the distance between cars is 57.74 meters.
The distance of the car that is making a depression angle of 30 degrees from the tower is 28.86 meters.
The distance of the car that is making a depression angle of 60 degrees from the tower is 86.6 meters.

Hence the correct answer is Option (D).

Note: Students should not be confused with the angle of elevation and the angle of depression. These are two different things. The angle of elevation is the rising angle generally, from the foot while the angle of depression is measured for the top of the tower.