Question

A straight highway leads to the foot of a tower of height 50 m. From the top of the tower, angles of the depressions of the two cars standing on the highway are $30^\circ$ and $60^\circ$. What is the distance between the cars ?
A. 43.3 m
B. 57.73 m
C. 86.6 m
D. 100 m

Answer 1

Hint: We had to only assume the distance between the tower and the cars and then by using the trigonometric formulas such as $\tan \theta = \dfrac{{{\text{Height}}}}{{{\text{Base}}}}$ and $\cot \theta = \dfrac{1}{{\tan \theta }} = \dfrac{{{\text{Base}}}}{{{\text{Height}}}}$. Then after solving these equations we will get the distance of cars from the tower.

Complete step-by-step answer:
Let us assume that the distance between Car A and tower is equal to x metres.
And the distance between Car B and Car A is equal to y metres.

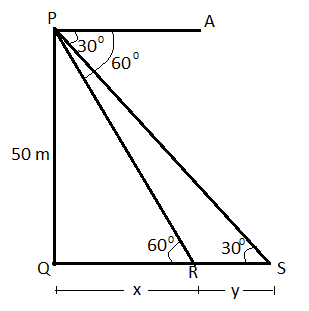
As we know that according to the theorem of alternate interior angles which states that if two lines are parallel then the opposite angles of the line joining opposite sides of the parallel lines must be equal.
So, $\angle APS = \angle PSQ$
And, $\angle APR = \angle PRQ$
Now in triangle PQR
$\tan 60^\circ = \dfrac{{{\text{Height}}}}{{{\text{Base}}}} = \dfrac{{PQ}}{{QR}} = \dfrac{{50}}{x}$ (1)
Now as we know that the value of $\tan 60^\circ$ is equal to $\sqrt 3$. So, equation 1 becomes,
$\sqrt 3 = \dfrac{{50}}{x}$
On cross-multiplying above equation. We get,
$x = \dfrac{{50}}{{\sqrt 3 }}$ (2)
Now in triangle PQS
$\tan 30^\circ = \dfrac{{{\text{Height}}}}{{{\text{Base}}}} = \dfrac{{PQ}}{{QS}} = \dfrac{{50}}{{x + y}}$
Now as we know that the value of $\tan 30^\circ$ is equal to $\dfrac{1}{{\sqrt 3 }}$.
So, putting the value of x from the equation 2 to the above equation. We get,
$\dfrac{1}{{\sqrt 3 }} = \dfrac{{50}}{{\dfrac{{50}}{{\sqrt 3 }} + y}}$
Now taking the LCM in the denominator of the RHS of the above equation and then solving. We get,
$\dfrac{1}{{\sqrt 3 }} = \dfrac{{50\sqrt 3 }}{{50 + y\sqrt 3 }}$
Now cross-multiplying the above equation. We get,

$$50 + y\sqrt 3 = 50 \times 3 \\\ y\sqrt 3 = 150 - 50 = 100 \\\ y = \dfrac{{100}}{{\sqrt 3 }} \\\$$

Now as we can see from the above figure that the distance between car A and car B is equal to y metres.
So, the distance between both cars will be equal to $\dfrac{{100}}{{\sqrt 3 }} = \dfrac{{100}}{{1.73}} = 57.73$metres.
Hence the correct option will be B.

Note:- Whenever we come up with this type of problem then we should remember that there is one another way to solve it. i.e. apart from using the trigonometric formula of $\tan \theta$ we can also use $\cot \theta$. And in that case according to trigonometric formula the values became vice versa i.e. $\tan 60^\circ$ will have same value as $\cot 30^\circ$ and $\cot 60^\circ$ will have the same value as $\tan 30^\circ$.