Question

A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.

Answer 1

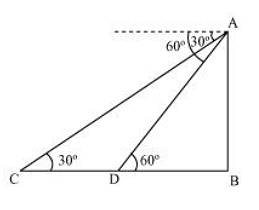
Initial position of the car is C, which changes to D after six seconds.

In ∆ADB,

$\frac{AB}{ DB} = tan 60^{\degree}$

$\frac{AB}{ DB} = \sqrt3$

$DB = \frac{AB} { \sqrt3}$

In ∆ABC,

$\frac{AB}{ BC}= tan 30^{\degree}$

$\frac{ AB }{ BD + DC} = \frac1{ \sqrt3}$

$AB \sqrt3 = BD + DC$

$AB \sqrt3 = \frac{AB }{\sqrt3} + DC$

$DC = AB \sqrt3 -\frac{ AB}{ \sqrt3} = AB (\sqrt3- \frac{1}{ \sqrt3})$

$$$DC= \frac{2AB}{ \sqrt3}$

Time taken by the car to travel distance DC= (i.e., $\frac{2AB}{ \sqrt3}$) = 6 seconds

Time taken by the car to travel distance DB (i.e., $\frac{AB}{ \sqrt3}$ ) = $\frac{6}{\frac{ 2AB}{ \sqrt3}} \times \frac{AB}{ \sqrt3}$ = $\frac 6{2}$ = 3 seconds.