Question

A straight conductor of weight$1\,N$ and length $0.5\,m$ is located in a place making an angle ${30^ \circ }$ with the horizontal so that it is perpendicular to a uniform magnetic field of induction $B = 0.109\,T$ .
Given that the conductor carries a current of $10\,A$ away from the reader and coefficient of static friction is point $0.1$ ,find the force needed to be applied parallel to the plane to sustain the conductor at rest
A. 0.63
B. 0.90
C. between 0.63 to 0.90
D. none of the above

Answer 1

Hint-
In order to solve this problem we need to analyse the forces acting on the conductor. Force on the conductor are force of gravity, force due to friction, normal reaction force, force due to magnetic field. The normal reaction force will be balanced by the components of magnetic field and gravity acting directly opposite to the normal force. The parallel force needed to sustain it at rest will be equal to the net force of the component of magnetic field and friction .

Complete step by step answer:
Given,
Weight of conductor, $w = 1\,N$
Length of conductor = $0.5\,m$
Angle made with horizontal =${30^0}$
Current carried by the conductor = $10\,A$
Let us analyse the forces acting on the conductor. Force on the conductor are force of gravity, force due to friction, normal reaction force, force due to magnetic field.
Force of gravity is given as $mg$
Force of normal reaction denoted as $N$
Force of friction is given as ${F_r} = \mu N$
Force of magnetic field is ${F_B} = Bil\cos \theta$. where $B$ is the magnetic field $i$ is the current, $l$ is the length of the conductor.
Let us analyse the diagrammatic representation.

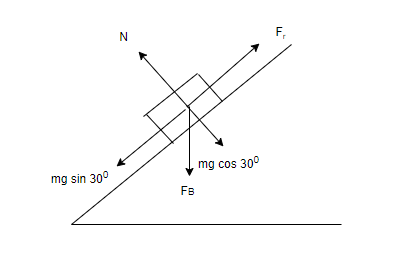
The normal reaction force is balanced by force due to magnetic field and cos component of force due to gravity.
$N = Bil\cos {30^0} + mg\cos {30^ \circ }$
$\rightarrow N = Bil\dfrac{{\sqrt 3 }}{2} + mg\dfrac{{\sqrt 3 }}{2}$ (1)
$\because \cos \,{30^ \circ } = \dfrac{{\sqrt 3 }}{2}$
If the force of the magnetic field and gravity is making it move downward then the force of friction will be acting upward. Let ${F_1}$ be the extra force needed to be applied parallel to stop motion of the conductor.
Force of friction and force acting upward is balanced by sine component of force of gravity and sine component of magnetic field.
Thus, we can write
${F_1} + \mu N = mg\sin {30^0} + Bil\sin {30^0}$
$\Rightarrow {F_1} + \mu N = \dfrac{{mg}}{2} + \dfrac{{Bil}}{2}$
$\because \sin \,{30^ \circ } = \dfrac{1}{2}$
$\rightarrow {F_1} = \dfrac{{mg}}{2} + \dfrac{{Bil}}{2} - \mu N$
Substitute value of $N$ from equation (1)
${F_1} = \dfrac{{mg}}{2} + \dfrac{{Bil}}{2} - \mu Bil\dfrac{{\sqrt 3 }}{2} - \mu mg\dfrac{{\sqrt 3 }}{2}$
Substitute given values.
${F_1} = \dfrac{1}{2} + \dfrac{{0.109 \times 10 \times 0.5}}{2} - 0.1 \times 0.109 \times 10 \times 0.5\dfrac{{\sqrt 3 }}{2} - 0.1 \times \dfrac{{\sqrt 3 }}{2}$
$\therefore {F_1} = 0.63N$
If the magnetic field is outwards the force on the conductor will be making it move upward. Force of friction will be downward. So the force of friction will be now in the opposite direction of the parallel force applied. Therefore we need to subtract it from parallel force .
${F_2} - \mu N = mg\sin {30^0} + Bil\sin {30^0}$
$\rightarrow {F_2} - \mu N = \dfrac{{mg}}{2} + \dfrac{{Bil}}{2}$
$\rightarrow {F_2} = \dfrac{{mg}}{2} + \dfrac{{Bil}}{2} + \mu Bil\dfrac{{\sqrt 3 }}{2} + \mu mg\dfrac{{\sqrt 3 }}{2}$
${F_2} = \dfrac{1}{2} + \dfrac{{0.109 \times 10 \times 0.5}}{2} + 0.1 \times 0.109 \times 10 \times 0.5\dfrac{{\sqrt 3 }}{2} + 0.1 \times \dfrac{{\sqrt 3 }}{2}$
$\therefore {F_2} = 0.90N$
Hence force should be between $0.63\,N$ to $0.90\,N$ .

Note: Take care of the direction of the forces acting while solving the problem. Since according to the direction of the magnetic field two directions of magnetic force can be taken. In the initial case when the magnetic field is taken inward direction then force acting will be downward then direction of friction will be upward. In the second case when motion of the conductor is upward then friction will be acting downward.