Question
Question: A straight bar of mass \(15kg\) and length \(2m\), at rest on a frictionless horizontal surface, rec...
A straight bar of mass 15kg and length 2m, at rest on a frictionless horizontal surface, receives an instantaneous impulse of 7Ns perpendicular to the bar. If the impulse is applied at the center of mass of the bar, the energy transferred is
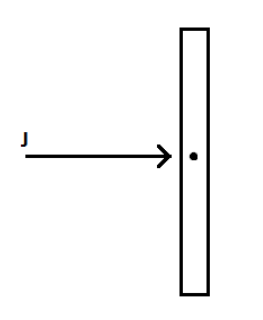
A) 1.6J
B) 1.9J
C) 3.8J
D) 2.5J
Solution
This problem can be solved by using the fact that the impulse is equal to the momentum change of a body and the direct formula relating the change in momentum to the change in kinetic energy of the body.
Formula used:
J=Δp
KE=2mp2
Complete answer:
The impulse J upon a body is equal to the change in momentum Δp of a body. That is,
J=Δp --(1)
Also, the momentum p of a body of mass m is related to its kinetic energy KE as
KE=2mp2 --(2)
Now, let us analyze the question.
The mass of the bar is m=15kg.
The impulse given to the body is J=7Ns.
Therefore, let the momentum change of the rod be Δp.
Let the initial momentum and initial kinetic energy of the body just before the impulse be pi and KEi respectively.
Let the final momentum and final kinetic energy of the rod just after receiving the impulse be pf and KEf respectively.
Now, using (1), we get
Δp=7Ns --(3)
Also, since the rod was at rest before the impulse, the initial momentum of the body is pi=0.
Therefore, using (2), we get the corresponding initial kinetic energy as KEi=2m02=0. --(4)
Now,
Δp=pf−pi
Putting (3) in the above equation, we get
7=pf−0
∴pf=7Ns --(5)
Therefore, the corresponding final kinetic energy of the rod will be
Kf=2m72=2×1549=3049J [Using (5)] --(6)
Now, the energy transferred to the rod by the impulse will be nothing but
ΔKE=KEf−KEi
Putting (4) and (6) in the above equation, we get
ΔKE=3049−0=3049≈1.6J
Hence, the energy transferred by the impulse to the rod is 1.6J.
Therefore, the correct option is A) 1.6J.
Note:
Students must note that impulse is nothing but the product of the force on a body and the time for which the force acts on the body. Impulse is usually the product of a large force and a small time period, that is, when a large force acts on a body for a small time (such as a cricket ball getting hit with a bat). Since, the force can be defined as the ratio of the momentum change of a body to the time in which the momentum changes, following that definition, the momentum change becomes equal to the product of the force and the time and hence, equal to the impulse on the body.
