Question

A stone tied to a string of length $L$ is whirled in a vertical circle with the other end of the string at the centre. At a certain instant of time the stone is at its lowest position and has a speed $u$. The magnitude of the change in velocity as it reaches a position, where the string is horizontal is
A. $\sqrt {{u^2} - 2gL}$
B. $\sqrt {2gL}$
C. $\sqrt {{u^2} - gL}$
D. $\sqrt {2({u^2} - gL)}$

Answer 1

The law of conservation of energy states that the total energy of an isolated system remains constant. So, the kinetic energy of the system initially must be equal to the final energy of the system i.e. the sum of potential energy and kinetic energy must be the same. Using their mathematical expressions we will derive the relation for the velocities in two states and thus the magnitude of the change in velocity.

Complete step-by-step answer:
It is given the question that stone at its lowest position and has a speed $u$ and height is $L$. Work done against gravity is the same at quarter position.

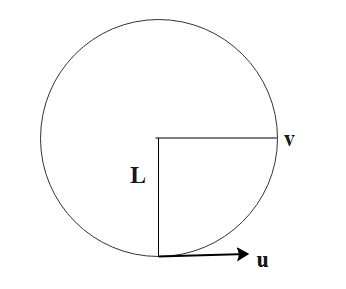
So, by conservation of energy we have,
\eqalign{ & \dfrac{1}{2}m{u^2} = \dfrac{1}{2}m{v^2} + mgh \cr & \Rightarrow \dfrac{1}{2}m{u^2} - \dfrac{1}{2}m{v^2} = mgh \cr & \Rightarrow \dfrac{1}{2}({u^2} - {v^2}) = gl \cr & \Rightarrow {v^2} - {u^2} = - 2gl \cr}
Now, adding $2{u^2}$ on both sides, we get:
\eqalign{ & {v^2} - {u^2} + 2{u^2} = 2{u^2} - 2gl \cr & \Rightarrow {v^2} + {u^2} = 2({u^2} - gl) \cr & \sqrt {{v^2} + {u^2}} = \sqrt {2({u^2} - gl)} \cr}
Therefore, the change in magnitude of velocity will be $\sqrt {2({u^2} - gl)}$
Hence, (D) is the correct option.

So, the correct answer is “Option D”.

Additional Information: A conservative force is defined as one for which work done by or against it depends only on the starting and ending points of a motion and not on the path taken. We can define a potential energy (PE) for any conservative force, because the work done against a conservative force to reach a final configuration depends on the configuration, not the path followed
A conservative force has following has following characteristics:

1. It is one dimensional since we get it from a scalar quantity.
2. Work done by a conservative force depends only on end points of the motion.
3. If the endpoints of the motion are the same i.e. the motion is in a closed loop, then the work done by a conservative force is zero.

Note: Since, we know that vector is a physical vector quantity, it comprises both magnitude and direction, to find the solution we only considered the magnitude.
According to the law of conservation of energy the total energy of an isolated system remains constant. It is said to be conserved over time. For example, the kinetic energy of a moving object transforms into heat energy when the object comes to rest by the virtue of friction.