Question

A stone of mass 1 kg is whirled in a horizontal circle attached at the end of a 1 m long string. If the string makes an angle of $30^\circ$ with the vertical, calculate the centripetal force acting on the stone. $\left( {9.8\,m/{s^2}} \right)$.$\left( {{\text{in }}N} \right)$
(A) 6.321
(B) 5.658
(C) 5.369
(D) 5.123

Answer 1

Draw the free body diagram of the forces acting on the stone. Balance the forces in the vertical direction to get the tension in the string and then use the value of tension force after balancing the forces in the horizontal direction.

Formula used:
${F_c} = \dfrac{{m{v^2}}}{r}$
Here, m is the mass of the body, v is the velocity and r is the radius of the circular motion.

Complete step by step answer:
A centripetal force is responsible for the circular motion of the body. Its acts towards the centre of the circular motion of the body.
The centripetal force is given by the expression,
${F_c} = \dfrac{{m{v^2}}}{r}$
Here, m is the mass of the body, v is the velocity and r is the radius of the circular motion.
Draw a free body diagram of the forces acting on a stone whirled in the horizontal circle as shown in the figure below,

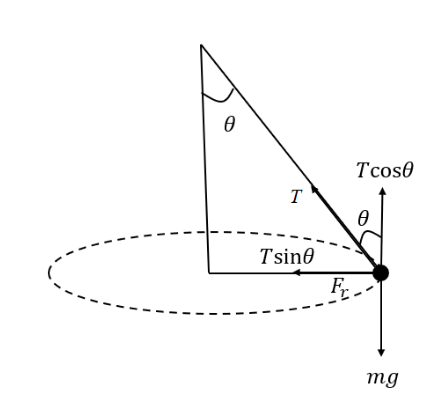
In the above figure, T is the tension in the string, $T\cos \theta$ is the vertical component of the tension, $T\sin \theta$ is the horizontal component of the tension, ${F_r}$ is the necessary centripetal force, and mg is the weight of the stone.
Balance the forces in the vertical direction as follows,
$T\cos \theta = mg$
$\Rightarrow T = \dfrac{{mg}}{{\cos \theta }}$
Substitute 1 kg for m, $9.8\,m/{s^2}$ for g and $30^\circ$ for $\theta$ in the above equation.
$T = \dfrac{{\left( {1\,kg} \right)\left( {9.8\,m/{s^2}} \right)}}{{\cos \left( {30^\circ } \right)}}$
$\Rightarrow T = \dfrac{{9.8\,N}}{{0.866}}$
$T = 11.316\,N$
Balance the forces in the horizontal direction as follows,
${F_r} = T\sin \theta$
Substitute 11.316 N for T and $30^\circ$ for $\theta$ in the above equation.
${F_r} = \left( {11.316\,N} \right)\sin \left( {30^\circ } \right)$
$\therefore {F_r} = 5.658\,N$
So, the correct answer is option (B).

Note: Always specify the direction of the forces as positive or negative. In the above free body diagram, the forces acting towards the left of the ball are taken to be negative. The forces acting in the upward direction are positive while the forces acting in the downward direction are negative.