Question

A stone of mass 1 kg is attached to the one end of a string of length 1 m and breaking strength 500 N, and is whirled in a horizontal circle on a frictionless table top. The other end of the string is kept fixed. Find the maximum speed the stone can attain, without breaking the string.

Answer 1

In this question, breaking point means that after 500 N if the tension is further increased, the rope will break. Use this information while making the net force equation. The centripetal force will be acting against the string.

Formula used:
For solving this question, we will be using the formula for the centripetal force, i.e.,
${{F}_{C}}=\dfrac{m{{v}^{2}}}{r}$

Complete answer:
Now, before we start solving the above question, let us take a look at all the given parameters

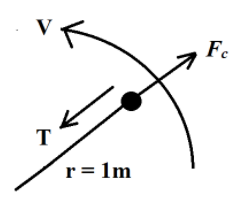
m = 1 kg, where m is the mass of the stone
r = 1 m. where r is the length of the rope
T = 500 N, where T is the breaking point of the rope, and in this case tension for calculating the maximum velocity
Now, as we are calculating the maximum speed attained,
We will take F = 500 N, as after 500 N the rope will break
So, We have
$F=\dfrac{m{{v}^{2}}}{r}$
$500=\dfrac{1\times {{v}^{2}}}{1}$
$500={{v}^{2}}$
$v=\sqrt{500}m/s$
$v=10\sqrt{5}m/s$
So, the maximum speed the stone can attain, without breaking the string will be, $v=10\sqrt{5}m/s$

Note:
If you are calculating the speed for any instance apart from the maximum velocity case, there will be one more variable in the equation, i.e., the weight of the stone. So the equation will become
$T+mg=\dfrac{m{{v}^{2}}}{r}$