Solveeit Logo
Login

Question

Question: A stone of density \(3000kg{{m}^{-3}}\) is lying submerged in water of density \(1000kg{{m}^{-3}}\)....

A stone of density 3000kgm−33000kg{{m}^{-3}} is lying submerged in water of density 1000kgm−31000kg{{m}^{-3}}. If the mass of the stone in air is 150 Kg, Calculate the force required to lift the stone. (g=10ms−2)\left( g=10m{{s}^{-2}} \right)

Explanation

Solution

Since, clearly there is water which is a fluid and in it the stone is present so, by the use of buoyancy force we will first find value of force applied by water on stone and after that we will subtract it by the formula of force.

Formula used:
B=ρVgB=\rho Vg, where B is buoyancy force, ρ\rho is a density and V is volume with g as gravitational force, Volume=massDensityVolume=\dfrac{mass}{Density}, F=mstoneg−BwaterF={{m}_{stone}}g-{{B}_{water}}

Complete answer:
According to the information given in the question we get to know that there is a stone which is in water and we need to find force that is needed to lift that stone. With the values given to us in question we have the following diagram.

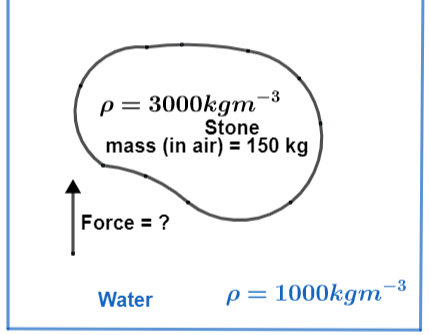
Mass: A mass is just another form of matter but it exists around us with no shape of its own. It never includes gravity and it is dented by m.
Density: If we take the ratio of mass over volume of any object then we will have the density of that object. This result into the value of average velocity will be calculated by dividing total mass of an object by its total volume only.
Volume: A volume is a simple ratio which can be taken out by keeping mass and density of an object in division.
Force: Any action of pushing off an object or pulling of an object is what we call as force. This is calculated by the product of an object’s mass and its acceleration.
Buoyancy force: It is a force that is applied on an object by any fluid. This force is exerted in upward direction. Its formula is as B=ρVgB=\rho Vg, where B is buoyancy force, ρ\rho is a density and V is volume with g as gravitational force.

As we are given that the mass and density of stone is 150 kg and 3000kgm−33000kg{{m}^{-3}} respectively, it will be easy for us to take out the value of its volume with the help of volume’s definition. Therefore, we get
Volume=massDensity ⇒Volume=150kg3000kgm−3 ⇒Volume=120m3 ⇒Volume=0.05m3 \begin{aligned} & Volume=\dfrac{mass}{Density} \\\ & \Rightarrow Volume=\dfrac{150kg}{3000kg{{m}^{-3}}} \\\ & \Rightarrow Volume=\dfrac{1}{20}{{m}^{3}} \\\ & \Rightarrow Volume=0.05{{m}^{3}} \\\ \end{aligned}
By formula of Buoyancy force we get
 Bwater=ρwaterVwatergwater ⇒Bwater=1000kgm−3×0.05m3×10ms−2 ⇒Bwater=500N \begin{aligned} & \,{{B}_{water}}={{\rho }_{water}}{{V}_{water}}{{g}_{water}} \\\ & \Rightarrow {{B}_{water}}=1000kg{{m}^{-3}}\times 0.05{{m}^{3}}\times 10m{{s}^{-2}} \\\ & \Rightarrow {{B}_{water}}=500N \\\ \end{aligned}
After eliminating buoyancy force we will get the actual value of the force needed here to lift the stone. Thus, the force is,
F=mstoneg−Bwater ⇒F=150kg×10ms−2−500N ⇒F=1000N \begin{aligned} & F={{m}_{stone}}g-{{B}_{water}} \\\ & \Rightarrow F=150kg\times 10m{{s}^{-2}}-500N \\\ & \Rightarrow F=1000N \\\ \end{aligned}
Hence, the required force will be 1000N to lift the stone discussed in question.

Note:
Buoyancy force is applied only by a fluid substance. Since, the stone is in water; the only force that was acting over it is force due to water. Therefore, the force that is applied by us will be different from that of water for which we deleted the value of buoyancy force in solution. We can see a clear conversion of kgms−2=Nkgm{{s}^{-2}}=N because these two are used as equivalent units. Since, the S.I the unit of force is Newton this is why this conversion was important here.