Question

A stone of 1kg is thrown with velocity of v=20m/s across the frozen surface of a lake and comes to rest after travelling a distance of 50m. What is the force of friction between the stone and ice?

Answer 1

When the object is thrown with some initial energy then the initial kinetic energy of the object is given by the half of the products of mass and square of velocity. We use the work energy theorem here, as the change in the kinetic energies is equal to the work done by frictional forces in contact.

Formula used: In Work energy theorem, the change in kinetic energies is equal to the work done by frictional forces .i.e.
$\vartriangle K.E=W$
Change in kinetic energies can be calculated as:
$\vartriangle K.E.={{K}_{i}}-{{K}_{f}}$

Complete step by step answer:
Work is the measure of force applied on the object. The figure shown below explains the given terms, also when it touches the surface there is some force of friction.

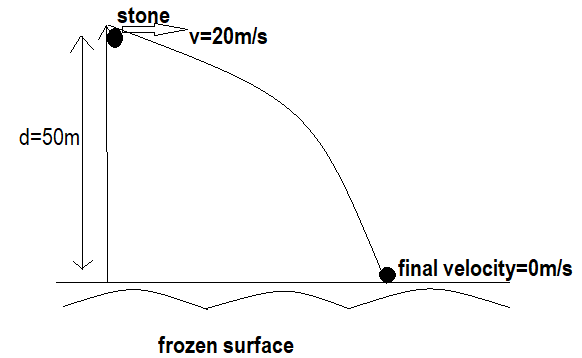
Here, we use the work energy theorem i.e. the change in kinetic energies is equal to the work done by the net forces on the body.
So, $\vartriangle K.E=W$
Also, the change in kinetic energies is calculated as:
$\vartriangle K.E.={{K}_{i}}-{{K}_{f}}$
The initial kinetic energy is given by:
$\begin{aligned} & {{K}_{i}}=(1/2)m{{v}^{2}} \\\ & {{K}_{i}}=(1/2)\times 1\times {{(20)}^{2}} \\\ & \Rightarrow {{K}_{i}}=200J \\\ \end{aligned}$
Now, when the stone touches the frozen surface then its final velocity becomes zero and the final kinetic energy to be zero.
So the change in kinetic energies is equal to:
$\begin{aligned} & \vartriangle K.E.={{K}_{i}}-{{K}_{f}} \\\ & \vartriangle K.E.=200J \\\ \end{aligned}$
Therefore work done by frictional forces is calculated as:
$\begin{aligned} & \vartriangle K.E=W \\\ & 200J=f\times d \\\ & 200J=f\times 50m \\\ & \Rightarrow f=4N \\\ \end{aligned}$
Hence, the force of friction between stone and ice comes out to be 4 Newton.

Note: When the body is thrown with some initial velocity, then this initial velocity corresponds to initial kinetic energy. When the body gets in contact with the surface, final velocity is zero results in final kinetic energy to be zero. From the work energy theorem, the work done by frictional force equals to change in kinetic energies.