Question

A stone is tied at one end of a 5 m long string and whirled in a vertical circle. The minimum speed required to just cross the topmost position is:
A. $5\,m{s^{ - 1}}$
B. $7\,m{s^{ - 1}}$
C. $57\,m{s^{ - 1}}$
D. $75\,m{s^{ - 1}}$

Answer 1

Balance the forces acting on the stone at the topmost position. The net acceleration of the stone at this point is zero. For the minimum velocity required to cross the topmost position, the tension in the string is zero. Solve the equation for velocity of the stone at the topmost position.

Formula used:
${F_C} = \dfrac{{m{v^2}}}{r}$
Here, m is the mass, g is the acceleration due to gravity and T is the tension in the string.

Complete step by step answer:
We know that in the vertical circular motion of a stone tied to the one end of the string, three forces acts on the system at every point in the circle: Centrifugal force on the stone, weight of the stone and tension in the string. We can draw the free body diagram of the forces acting on the system of stone revolving in the vertical circle as below,

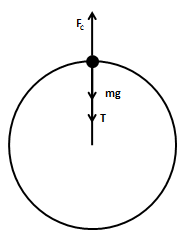
We balance the forces acting on the stone in the vertical direction as follows,

${F_C} = mg + T$

Here, m is the mass of the stone, g is the acceleration due to gravity and T is the tension in the string.
We know that the magnitude of the centrifugal force is the same as centripetal force. The expression for centripetal force on the stone is,

${F_C} = \dfrac{{m{v^2}}}{r}$

Here, v is the velocity of the stone at the topmost point and r is the radius of the circle.
Therefore, we can write,
$\dfrac{{m{v^2}}}{r} = mg + T$
At the topmost position in the vertical circle, for the minimum velocity, the tension in the string will be zero. Therefore, we substitute 0 for T in the above equation.
$\dfrac{{m{v^2}}}{r} = mg$
$\Rightarrow \dfrac{{{v^2}}}{r} = g$
$\Rightarrow v = \sqrt {rg}$
We substitute 5 m for r and $10\,m/{s^2}$ for g in the above equation.
$\Rightarrow v = \sqrt {\left( 5 \right)\left( {9.8} \right)}$
$\Rightarrow v = \sqrt {49}$
$\Rightarrow v = 7\,m{s^{ - 1}}$
Therefore, the velocity of the stone should be 7 m/s to just cross the topmost position.

So, the correct answer is option (B).

Note:
In the above solution, we have used Newton’s second law of motion to balance the forces on the stone. The acceleration term is absent in the equation since the stone at the topmost position has its motion towards right and forces are acting in the downward direction. Students should note that the direction of the centripetal force towards the centre of the circular motion and the direction of the centrifugal force which is acting on the stone has direction opposite to the direction of the centripetal force.