Question

A stone is thrown vertically upwards and it reaches a maximum height of $30{\text{ }}m$. What was its initial velocity?

Answer 1

In the given question the maximum height attained by the stone is given. Hence, the stone follows projectile motion. We will use the formula used to find the maximum height and hence by substituting the values we will find the answer.

Complete answer:
It is given in the question that the maximum height attained by the stone is $30{\text{ }}m$.

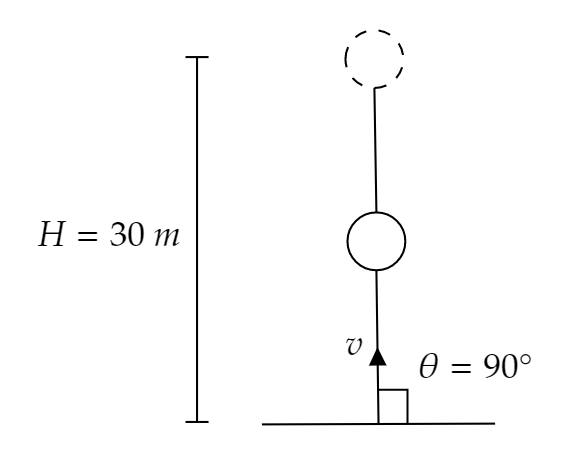
The stone thus follows projectile motion.
The formula to find the maximum height attained by a particle in projectile motion is,
$H = \dfrac{{{v^2}{{\sin }^2}\theta }}{{2g}} - - - - \left( 1 \right)$
The variables are defined as,
$H =$ maximum height attained by the body that is thrown
$v =$ initial velocity at which the body is thrown
$\theta =$ angle at which the body is thrown
$g =$ acceleration due to gravity
The maximum height $H = 30{\text{ }}m$
The angle of projection $\theta = {90^ \circ }$ as the question is mentioned that the stone is thrown vertically upwards.
$g = 9.8{\text{ }}\dfrac{m}{{{s^2}}}$
Substituting the values in equation $\left( 1 \right)$ we get,
$30 = \dfrac{{{v^2}{{\sin }^2}{{90}^ \circ }}}{{2 \times 9.8}}$
From trigonometric values we know, $\sin {90^ \circ } = 1$. Now, we get,
${v^2} = 588$
Square root of the given equation we get,
$v = 24.24$
The initial velocity of the stone which is thrown vertically upward is $24.24{\text{ }}\dfrac{m}{s}$.

Note: Students tend to make errors while solving these types of questions because they fail to apply the formulas correctly, as well as to use the correct sign based on the direction of motion of the object. So, they should make sure to understand the problem's scenario clearly and then solve it without any error in calculation.