Solveeit Logo
Login

Question

Question: A stone is thrown vertically up from the tower of height \(25{\text{ }}m\) with a speed of \(20{\tex...

A stone is thrown vertically up from the tower of height 25 m25{\text{ }}m with a speed of 20 ms20{\text{ }}\dfrac{m}{s} time taken to reach the ground?

Explanation

Solution

First of all, we have to find the height which is achieved by the stone when thrown vertically upwards. Then we have to find the total height required by the stone to reach the ground. By using motion’s equation we will find separate time intervals. Then by their algebraic sum we will find the total time required to reach the ground.

Complete step by step answer:

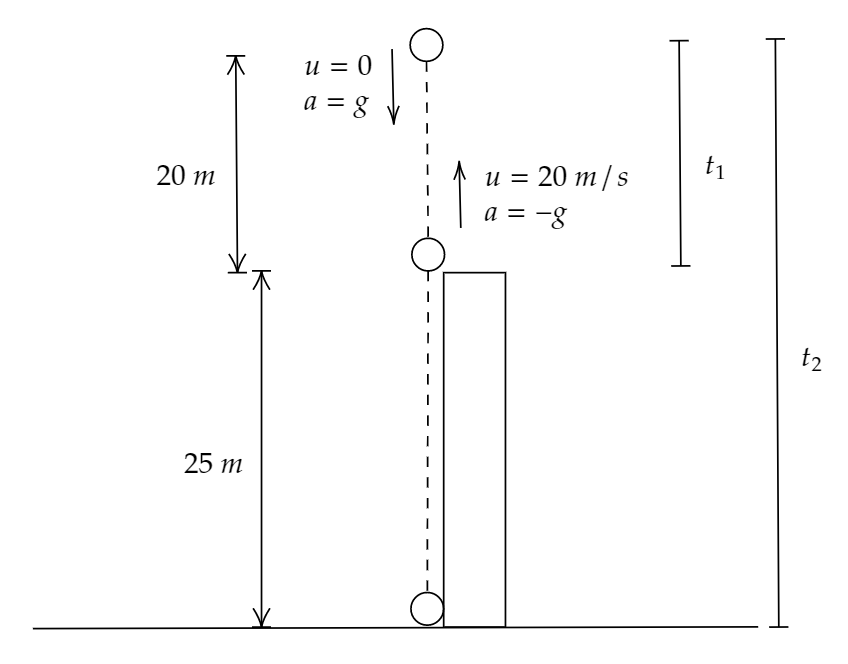
It is given that the stone is thrown upward from a tower of height 25 m25{\text{ }}m with a speed of 20 ms20{\text{ }}\dfrac{m}{s}.
Let us consider that the height which the stone attains when it is thrown vertically from the tower be hh.
From the Motion’s Equation, we get,
v2−u2=2as−−−(1){v^2} - {u^2} = 2as - - - \left( 1 \right)
The variables are defined as,
v=v = final velocity achieved by the object
u=u = initial velocity applied to the object
a=a = acceleration of the object
s=s = distance covered by the object
For the given question, when the stone is thrown,
The final velocity v=0v = 0
Initial velocity is given as u=20 msu = 20{\text{ }}\dfrac{m}{s}
Acceleration of the stone is the acceleration due to gravity a=−g=−10 ms2a = - g = - 10{\text{ }}\dfrac{m}{{{s^2}}}
The height achieved by the stone s=hs = h
Substituting the values in equation (1)\left( 1 \right) we get,
0−(20)2=2×−10×h0 - {\left( {20} \right)^2} = 2 \times - 10 \times h
⇒h=−400−20=20\Rightarrow h = \dfrac{{ - 400}}{{ - 20}} = 20
The height attained by the stone is 20 m20{\text{ }}m.
Let the time required to reach height 20 m20{\text{ }}m by the stone be t1{t_1}.
From the relation v=u+at−−−−(2)v = u + at - - - - \left( 2 \right) where v=v = final velocity, u=u = initial velocity, a=a = acceleration and t=t = time.
Here, v=0, u=20, a=−g=−10, t=t1v = 0,{\text{ }}u = 20,{\text{ }}a = - g = - 10,{\text{ }}t = {t_1}
Substituting the value in equation (2)\left( 2 \right) we get,
0=20−10t10 = 20 - 10{t_1}
⇒t1=2 s\Rightarrow {t_1} = 2{\text{ }}s
Now, the distance to be covered by the stone to reach ground=(20+25)m=45 m = \left( {20 + 25} \right)m = 45{\text{ }}m
Now, we have to use the relation s=ut+12at2−−−−(3)s = ut + \dfrac{1}{2}a{t^2} - - - - \left( 3 \right), where s=s = distance to be covered=45 m = 45{\text{ }}m, t=t = time required=t2 = {t_2}, initial velocity =u=0 ms = u = 0{\text{ }}\dfrac{m}{s} and a=a = acceleration=g=10 ms2 = g = 10{\text{ }}\dfrac{m}{{{s^2}}}
Substituting all the values in equation (3)\left( 3 \right) we get,
45=0+12×10×t2245 = 0 + \dfrac{1}{2} \times 10 \times t_2^2
⇒t2=3 s\Rightarrow {t_2} = 3{\text{ }}s
The total time required by the stone to reach the ground=(t1+t2)=(2+3)=5 s = \left( {{t_1} + {t_2}} \right) = \left( {2 + 3} \right) = 5{\text{ }}s.
The stone takes 5 s5{\text{ }}s to reach the ground.

Note: It must be noted that the acceleration of the particle is considered to be acceleration due to gravity as the stone thrown and returned is in vertical direction. When the stone is thrown upward the acceleration is negative as it acts opposite to the direction of the acceleration due to gravity.