Question

A stone is attached to the end of a string and whirled in horizontal circle with uniform speed then
(A) Its linear and angular momentum is constant.
(B) Only linear momentum is constant.
(C) Its angular momentum is constant but linear momentum is variable.
(D) Both are variable.

Answer 1

Angular momentum was introduced as the rotational equivalent of linear momentum. As linear momentum is defined by mass times its velocity, angular momentum is defined as the moment of inertia times the angular velocity in rotational motion of a body. We will solve this problem using the definitions of linear and angular momentum.

Formula used: Linear momentum,

& p=m\vec{v} \\\ & \\\ \end{aligned}$$ Angular momentum, $\vec{L}=m(\vec{r}\times \vec{v})$ **Complete step by step answer:** 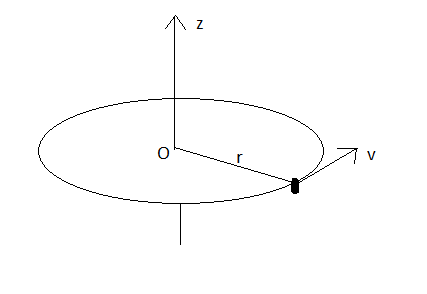 Fig: stone attached to the end of the string and swirled in a circle with uniform speed Let the mass of the stone be m, and its velocity be v and the radius of the circle be r. From the above figure, we see that although the stone is moving with constant speed, the direction of the stone changes as the stone moves in a circular motion. $\therefore $ We can say that the velocity of the stone is not constant and is changing, so we can conclude that the linear momentum given by. $$\begin{aligned} & p=m\vec{v} \\\ & \\\ \end{aligned}$$ Is not constant, since the mass is constant here but the velocity is varying. On the other hand, its angular momentum is given by, $\vec{L}=m(\vec{r}\times \vec{v})$ Here, mass m is constant but the cross product of radius vector and velocity vector is given in the perpendicular direction of the horizontal surface, that is, the cross product is given in the z direction. So here the angular momentum remains constant. Thus, it is clear that the angular momentum is constant but the linear momentum is variable. **So, the correct answer is “Option C”.** **Additional Information:** Angular momentum is an extensive quantity. The total angular momentum of any composite system is the sum of the angular momentum of the constituent parts. The same can be said about linear momentum. **Note:** In this problem, care should be taken while finding the direction. The direction must be taken into account in both linear and angular momentum because we are dealing with vectors in this problem. In case of angular momentum, we always consider the cross product of 2 vectors and that must be kept in mind.