Question

A stone is allowed to fall from the top of a tower of height 100m and at the same time, another stone is projected vertically upwards from the ground with a velocity of 25m/s. Calculate when and where the two stones will meet.

Answer 1

Hint: The point of collision can be considered as $x$ and the time of the collision as $t$. Then we can find $x$ and $t$ using the two sets of data given. We can simplify things by realizing that there is no relative acceleration between the two stones.

Complete step by step answer:
Let us say that the two stones hit each other at a distance $x$ above the ground at time $t$. Also, let us say this point of collision is P.

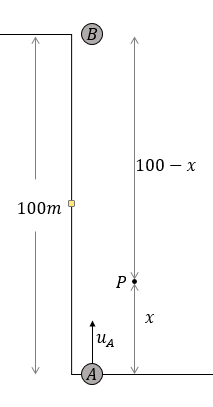
For stone $A$ to reach$P$, it travelled upwards with a constant downward acceleration. So the displacement $x$ and time $t$ is related as $x = {u_A}t - \dfrac{1}{2}g{t^2}$ …(1)
Here g is the acceleration due to gravity and ${u_A}$ is the initial upwards velocity given.

Similarly, for the stone dropped from the top, it has no downward initial velocity but only a downward acceleration. Also, we know the tower is 100m high. So if stone A had travelled $x$ distance, stone B should have travelled $100 - x\;m$. So the displacement of stone $B$ is given as :
$100 - x = \dfrac{1}{2}a{t^2}$ …(2)

Now, let us add equations (1) and (2).

$100 - x + x = {u_A}t + \dfrac{1}{2}a{t^2} - \dfrac{1}{2}a{t^2}$
$100 = {u_A}t$
Let us now substitute the values of ${u_B}$ and ${u_A}$ to get the time taken.
$100 = (25)t$
$t = \dfrac{{100}}{{25}} = 4s$

Now, the position of collision, $x$ can be found by substituting the value of $t$ obtained in equation (1)
$x = 25 \times 4 - \dfrac{1}{2} \times 9.8 \times {\left( 4 \right)^2}$
$x = 100 - 78.4 = 21.6m$

Note: Here, both objects experience the same acceleration of $g$ in the same direction. So we can say that there is no relative acceleration between the two stones. So from stone A's perspective, stone B is approaching with zero acceleration (constant speed).
Here since the relative velocity of stone A with respect to stone B is ${u_B} - {u_A} = 0 - 25 = - 25m/s$ towards stone B. With this in mind, we can easily calculate the time of the collision. We have two bodies approaching each other at $125m/s$ with $100m$ separation. The time taken to collide would be $t = \dfrac{{{\text{distance}}}}{{{\text{speed}}}} = \dfrac{{100}}{{25}} = 4s$.