Question

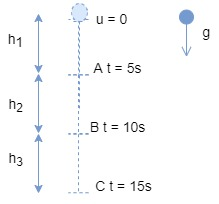
A stone falls freely under gravity. It covers distance ${{h}_{1}}$ ${{h}_{2}}$ and ${{h}_{3}}$ in the first 5 seconds, the next 5 seconds and the next 5 seconds respectively. The relation between ${{h}_{1}}$ , ${{h}_{2}}$ and ${{h}_{3}}$ is:
(A) ${{h}_{1}}=2{{h}_{2}}=3{{h}_{3}}$
(B) ${{h}_{1}}=\dfrac{{{h}_{2}}}{3}=\dfrac{{{h}_{3}}}{5}$
(C) ${{h}_{2}}=3{{h}_{1}}\text{ }and\text{ }{{h}_{3}}=3{{h}_{2}}$
(D) ${{h}_{1}}={{h}_{2}}={{h}_{3}}$

Answer 1

We can use position time relation which is given by
$S=ut+\dfrac{1}{2}a{{t}^{2}}$
Here, S is distance travelled in time t,
u is the initial velocity,
a is the acceleration and t is time taken.
In case of free fall, if downward direction is taken positive and object is released from rest, then
$u=0,\text{ }a=g=10m/{{s}^{2}},\text{ }S=h$
In case of free fall, if downward direction is taken negative and object is released from set, then
$u=0,\text{ }a=-g=-10m/{{s}^{2}},\text{ }S=-h$ .

Complete step by step solution
We have, given
Stone is falling freely under gravity.
It means, if we will take downward as negative
Then, $a=-g$
$S=-{{h}_{1}}$
Case I: Where ${{h}_{1}}$ is the distance covered in first seconds,
Here, stone is falling freely hence take initial velocity as zero.
$u=0$ , t=5s is given
Then use distance/position-time relation
$S=ut+\dfrac{1}{2}a{{t}^{2}}$
Here, $a=-g$ , means acceleration due to gravity.
Put all the above values:

${{h}_{1}}=\dfrac{25}{2}g$ ; $-{{h}_{1}}=0\left( 5 \right)+\dfrac{1}{2}\left( -g \right){{\left( 5 \right)}^{2}}$
$-{{h}_{1}}=-\dfrac{1}{2}\times g{{\left( 25 \right)}^{{}}}$
${{h}_{1}}=\dfrac{25}{2}g$ ----------(2)
Now in Case II:
Distance travelled by stone in next 5 seconds,
Now total distance covered will be, $S=-\left( {{h}_{1}}+{{h}_{2}} \right)$ [negative sign shows just direction of measurement]
And total time taken, t=5+5=10s
Put the above values in eq, (1)
$-\left( {{h}_{1}}+{{h}_{2}} \right)=0\left( 10 \right)+\dfrac{1}{2}\left( -g \right){{\left( 10 \right)}^{2}}$
$\left( {{h}_{1}}+{{h}_{2}} \right)=\dfrac{1}{2}g\left( 100 \right)=\dfrac{100}{2}g$ ---------(3)
Case III:
Distance travelled by stone in next 5 seconds,
Total distance covered $S=-\left( {{h}_{1}}+{{h}_{2}}+{{h}_{3}} \right)$
Total time taken $t=5+5+5=15s$
Put the values in eq. (1)
$-\left( {{h}_{1}}+{{h}_{2}}+{{h}_{3}} \right)=-\dfrac{1}{2}g{{\left( 15 \right)}^{2}}$
$\left( {{h}_{1}}+{{h}_{2}}+{{h}_{3}} \right)=\dfrac{225}{2}g$ ------- (4)
Solve eq. (2) and (3)
$\left( {{h}_{1}}+{{h}_{2}} \right)-{{h}_{1}}=\dfrac{100}{2}g-\dfrac{25}{2}g$
${{h}_{2}}=\dfrac{75}{2}g$ -------- (5)
Solve eq. (3) and (4),
$\left( {{h}_{1}}+{{h}_{2}}+{{h}_{3}} \right)-\left( {{h}_{1}}+{{h}_{2}} \right)=\dfrac{225}{2}g-\dfrac{100}{2}g$
${{h}_{3}}=\dfrac{125}{2}g$ --------- (6)
Write eq. (5) and (6) in terms of
${{h}_{2}}=\dfrac{25}{2}\times 3g\to {{h}_{2}}=3{{h}_{1}}$ ---------- (7)
${{h}_{3}}=\dfrac{25}{2}\times 5g\to {{h}_{3}}=5{{h}_{1}}$ ----------- (8)
From eq. (7) and (8),
${{h}_{1}}={{\dfrac{{{h}_{2}}}{3}}_{{}}}=\dfrac{{{h}_{3}}}{5}$ This is required result.
Therefore option (B) is the correct answer.

Note
We can also, use direct formula, Distance travelled in the second by,
${{D}_{n}}=u+\dfrac{a}{2}\left( 2n-1 \right)$
Here, n is nth second, above question n is given as 5s.
Using the above formula we will get the same answer.